Exercises:Mond - Topology - 1

Section B

Exercises 6, 7 and 8 make use of the compact-to-Hausdorff theorem

Question 6

Part I

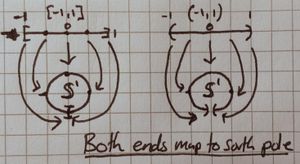
Find a surjective continuous mapping from $[-1,1]\subset\mathbb{R}$ to the unit circle, $\mathbb{S}^1$ such that it is injective except for that it sends $-1$ and $1$ to the same point in $\mathbb{S}^1$. Definitions may be explicit or use a picture

Solution

Take -1 to any point on the circle (we pick the south pole in this diagram), then go around the circle clockwise at a constant speed such that by $f(1)$ one has done a full revolution and is back at the starting point.

The right-hand-side is intended to demonstrate that the interval $(-1,1)$ to the circle without the south-pole is bijective, ie it is injective and surjective, so the diagram on the left is "almost injective" in that it is injective everywhere except that it maps $-1$ and $1$ both to the south pole.
As required

We shall define $f:[-1,1]\rightarrow\mathbb{S}^1$ to be such a map:

• $f:t\mapsto\begin{pmatrix}-\sin(\pi(t+1))\\-\cos(\pi(t+1))\end{pmatrix}$, this starts at the point $(1,0)$ and goes anticlockwise around the circle of unit radius once.
  • Note: I am not asked to show this is continuous, merely exhibit it.
  • Note: The reason for the odd choice of $\sin$ for the $x$ coordinate, and the minus signs is because my first choice was $f:t\mapsto\begin{pmatrix}\cos(\pi(t+1))\\\sin(\pi(t+1))\end{pmatrix}$, however that didn't match up with the picture. The picture goes clockwise from the south pole, this would go anticlockwise from the east pole.

Part 2

Define an equivalence relation on $[-1,1]$ by declaring $-1\sim 1$, use part 1 above and applying the topological version of passing to the quotient to find a continuous bijection: $(:\frac{[-1,1]}{\sim}\rightarrow\mathbb{S}^1)$

Solution

We wish to apply passing to the quotient. Notice:

1. we get $\pi:[-1,1]\rightarrow\frac{[-1,1]}{\sim}$, $\pi:x\mapsto [x]$ automatically and it is continuous.
2. we've already got a map, $f$, of the form $(:[-1,1]\rightarrow\mathbb{S}^1)$

In order to use the theorem we must show:

• "$f$ is constant on the fibres of $\pi$", that is:
  • $\forall x,y\in [-1,1][\pi(x)=\pi(y)\implies f(x)=f(y)]$
• Proof:
  • Let $x,y\in[-1,1]$ be given
    • Suppose $\pi(x)\ne\pi(y)$, by the nature of implies we do not care about the RHS of the implication, true or false, the implication holds, so we're done
    • Suppose $\pi(x)=\pi(y)$, we must show that this means $f(x)=f(y)$
      • It is easy to see that if $x\in(-1,1)\subset\mathbb{R}$ then $\pi(x)=\pi(y)\implies y=x$
        • By the nature of $f$ being a function (only associating an element of the domain with one thing in the codomain) and having $y=x$ we must have: $f(x)=f(y)$
      • Suppose $x\in\{-1,1\}$, it is easy to see that then $\pi(x)=\pi(y)\implies y\in\{-1,1\}$
        • But $f(-1)=f(1)$ so, whichever the case, $f(x)=f(y)$

We may now apply the theorem to yield:

• a unique continuous map, $\overline{f}:[-1,1]/\sim\rightarrow\mathbb{S}^1$ such that $f=\overline{f}\circ\pi$

The question requires us to show this is a bijection, we must show that $\newcommand{\fbar}{\bar{f} }\fbar$ is both injective and surjective:

1. Surjective: $\forall y\in \mathbb{S}^1\exists x\in \frac{[-1,1]}{\sim}[\fbar(x)=y]$
   • There are two ways to do this:
     1. Note that (from passing to the quotient) that if $f$ is surjective, then the resulting $\fbar$ is surjective.
     2. Or the long way of showing the definition of $\fbar$ being a surjection, $\forall y\in\mathbb{S}^1\exists x\in\frac{[-1,1]}{\sim}[\fbar(x)=y]$
        • Let $y\in \mathbb{S}^1$ be given.
          • Note that $f$ is surjective, and $f=\fbar\circ\pi$, thus $\exists p\in[-1,1]$ such that $p=f^{-1}(y)=(\fbar\circ\pi)^{-1}(y)=\pi^{-1}(\fbar^{-1}(y))$, thus $\pi(p)=\fbar^{-1}(y)$
          • Choose $x\in[-1,1]/\sim$ to be $\pi(p)$ where $p\in[-1,1]$ exists by surjectivity of $f$ and is such that $f(p)=y$
            • Now $\fbar(\pi(p))=f(p)$ (by definition of $\fbar$) and $f(p)=y$, as required.
2. Injective:
   • Let $x,y\in\frac{[-1,1]}{\sim}$ be given. We wish to show that $\fbar(x)=\fbar(y)\implies x=y$
     • Suppose $\fbar(x)\ne\fbar(y)$, then we're done, as by the nature of logical implication we do not care about the right hand side.
       • Note though, by the definition of $\fbar$ being a function we cannot have $x=y$ in this case! As a function must map each element of the domain to exactly one thing of the codomain. Anyway!
     • Suppose $\fbar(x)=\fbar(y)$, we must show that in this case we have $x=y$.
       • By surjectivity of $\pi:[-1,1]\rightarrow\frac{[-1,1]}{\sim}$ we see $\exists a\in [-1,1]\big[\pi(a)=x\big]$ and $\exists b\in [-1,1]\big[\pi(b)=y\big]$
         • Notice now we have $\fbar(x)=\fbar(\pi(a))$ and that (from the passing to the quotient part of obtaining $\fbar$) we have $f=\fbar\circ\pi$, this means:
           • $\fbar(x)=\fbar(\pi(a))=f(a)$, we also have $\fbar(y)=\fbar(\pi(b))=f(b)$ from the same thoughts, but using $y$ and $b$ instead of $x$ and $a$.
         • In particular: $f(a)=f(b)$
         • Now we have two cases, $a\in(-1,1)$ and $a\in\{-1,1\}$, we shall deal with them separately.
           1. We have $f(a)=f(b)$, suppose $a\in(-1,1)$
              • Recall that our very definition of $f$ required it to be "almost injective", specifically that $f\big\vert_{(-1,1)}:(-1,1)\rightarrow\mathbb{S}^1$ was injective (and that it was only "not injective" on the endpoints)
              • As $f$ is "injective in this range" we see that to have $f(a)=f(b)$ means $a=b$ (by injectiveness of $f\big\vert_{(-1,1)}$)
                • As $a=b$ we see $y=\pi(b)=\pi(a)=x$ and conclude $y=x$ - as required.
           2. We have $f(a)=f(b)$, and this time $a\in\{-1,1\}$ instead
              • Again by definition of $f$, we recall $f(-1)=f(1)$ - it maps the endpoints of $[-1,1]$ to the same point in $\mathbb{S}^1$.
              • To have $f(a)=f(b)$ clearly means that $b\in\{-1,1\}$ (regardless of what value $a\in\{-1,1\}$ takes)
                • But $\pi(a)=[a]=\{-1,1\}$ and also $\pi(b)=[b]=\{-1,1\}$
                • So we see $y=\pi(b)=\{-1,1\}=\pi(a)=x$, explicitly: $x=y$, as required
         • We have shown that in either case $x=y$
   • Since $x,y\in\frac{[-1,1]}{\sim}$ was arbitrary, we have shown this for all $x,y$. The very definition of $\fbar$ being injective.

Thus $\fbar$ is a bijection

Part 3

Show that $[-1,1]/\sim$ is homeomorphic to $\mathbb{S}^1$

Solution

To apply the "compact-to-Hausdorff theorem" we require:

1. A continuous bijection, which we have, namely $\fbar:\frac{[-1,1]}{\sim}\rightarrow\mathbb{S}^1$
2. the domain space, $\frac{[-1,1]}{\sim}$, to be compact, and
3. the codomain space, $\mathbb{S}^1$, to be Hausdorff

We know the image of a compact set is compact, and that closed intervals are compact in $\mathbb{R}$, thus $[-1,1]/\sim=\pi([1-,1])$ must be compact. We also know $\mathbb{R}^2$ is Hausdorff and every subspace of a Hausdorff space is Hausdorff, thus $\mathbb{S}^1$ is Hausdorff.

We apply the theorem:

• $\fbar$ is a homeomorphism

Question 7

Let $D^2$ denote the closed unit disk in $\mathbb{R}^2$ and define an equivalence relation on $D^2$ by setting $x_1\sim x_2$ if $\Vert x_1\Vert=\Vert x_2\Vert=1$ ("collapsing the boundary to a single point"). Show that $\frac{D^2}{\sim}$ is homeomorphic to $\mathbb{S}^2$ - the sphere.

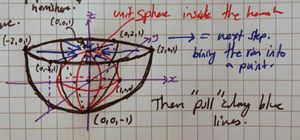
• Hint: first define a surjection $(:D^2\rightarrow\mathbb{S}^2)$ mapping all of $\partial D^2$ to the north pole. This may be defined using a good picture or a formula.

Solution

The idea is to double the radius of $D^2$, then pop it out into a hemisphere, then pull the rim to a point

Picture showing the "expanding $D^2$", the embedding-in-$\mathbb{R}^3$ part, and the "popping out"

Definitions:

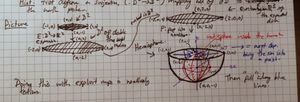
• $H$ denotes the hemisphere in my picture.
• $E:D^2\rightarrow H$ is the composition of maps in my diagram that take $D^2$, double its radius, then embed it in $\mathbb{R}^3$ then "pop it out" into a hemisphere. We take it as obvious that it is a homeomorphism
• $f':H\rightarrow\mathbb{S}^2$, this is the map in the top picture. It takes the hemisphere and pulls the boundary/rim in (along the blue lines) to the north pole of the red sphere. $f'(\partial H)=(0,0,1)\in\mathbb{R}^3$, it should be clear that for all $x\in H-\partial H$ that $f'(x)$ is intended to be a point on the red sphere and that $f'\big\vert_{H-\partial H}$ is injective. It is also taken as clear that $f'$ is surjective
• Note: Click the pictures for a larger version
• $\frac{D^2}{\sim}$ and $D^2/\sim$ denote the quotient space, with this definition we get a canonical projection, $\pi:D^2\rightarrow D^2/\sim$ given by $\pi:x\mapsto [x]$ where $[x]$ denotes the equivalence class of $x$
• Lastly, we define $f:D^2\rightarrow\mathbb{S}^2$ to be the composition of $E$ and $f'$, that is: $f:=f'\circ E$, meaning $f:x\mapsto f'(E(x))$

The situation is shown diagramatically below:

• $\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f:=f'\circ E} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} }$

Outline of the solution:

• We then want apply the passing to the quotient theorem to yield a commutative diagram: $\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} \ar@{.>}[urr]_{\bar{f} } }$
  • The commutative diagram part merely means that $f=\bar{f}\circ\pi$. We get $f=\bar{f}\circ\pi$ as a result of the passing-to-the-quotient theorem.
  • We take this diagram as showing morphisms in the TOP category, meaning all arrows shown represent continuous maps. (Obviously...)
• Lastly, we will show that $\bar{f}$ is a homeomorphism using the compact-to-Hausdorff theorem

Solution body

First we must show the requirements for applying passing to the quotient are satisfied.

• We know already the maps involved are continuous and that $\pi$ is a quotient map. We only need to show:
  • $f$ is constant on the fibres of $\pi$, which is equivalent to:
    • $\forall x,y\in D^2[\pi(x)=\pi(y)\implies f(x)=f(y)]$
• Let us show this remaining condition:
  • Let $x,y\in D^2$ be given.
    • Suppose $\pi(x)\ne\pi(y)$, then by the nature of logical implication the implication is true regardless of $f(x)$ and $f(y)$'s equality. We're done in this case.
    • Suppose $\pi(x)=\pi(y)$, we must show that in this case $f(x)=y(y)$.
      • Suppose $x\in D^2-\partial D^2$ (meaning $x\in D^2$ but $x\notin \partial D^2$, ie $-$ denotes relative complement)
        • In this case we must have $x=y$, as otherwise we'd not have $\pi(x)=\pi(y)$ (for $x\in D^2-\partial D^2$ we have $\pi(x)=[x]=\{x\}$, that is that the equivalence classes are singletons. So if $\pi(x)=\pi(y)$ we must have $\pi(y)=[y]=\{x\}=[x]=\pi(x)$; so $y$ can only be $x$)
        • If $x=y$ then by the nature of $f$ being a function we must have $f(x)=f(y)$, we're done in this case
      • Suppose $x\in \partial D^2$ (the only case not covered) and $\pi(x)=\pi(y)$, we must show $f(x)=f(y)$
        • Clearly if $x\in\partial D^2$ and $\pi(x)=\pi(y)$ we must have $y\in\partial D^2$.
          • $E(x)$ is mapped to the boundary/rim of $H$, as is $E(y)$ and $f'(\text{any point on the rim of }H)=(0,0,1)\in\mathbb{R}^3$
          • Thus $f'(E(x))=f'(E(y))$, but $f'(E(x))$ is the very definition of $f(x)$, so clearly:
            • $f(x)=f(y)$ as required.

We may now apply the passing to the quotient theorem. This yields:

• A continuous map, $\bar{f}:D^2/\sim\rightarrow\mathbb{S}^2$ where $f=\bar{f}\circ\pi$

$\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} \ar@{.>}[urr]_{\bar{f} } }$
Commutative diagram of situation (all maps are continuous)

We now have the situation of the diagram on the right, restated from above for convenience.

In order to apply the compact-to-Hausdorff theorem and show $\bar{f}$ is a homeomorphism we must show it is continuous and bijective. We already have continuity (as a result of the passing-to-the-quotient theorem), we must show it is bijective.

We must show $\bar{f}$ is both surjective and injective:

1. Surjectivity: We can get this from the definition of $\bar{f}$, recall on the passing to the quotient (function) page that:
   • if $f$ is surjective then $\bar{f}$ (or $\tilde{f}$ as the induced function is on that page) is surjective also
     • I've already done it "the long way" once in this assignment, and I hope it is not frowned upon if I decline to do it again.
2. Injectivity: This follows a similar to gist as to what we've done already to show we could apply "passing to the quotient" and for the other questions where we've had to show a factored map is injective. As before:
   • Let $x,y\in\frac{D^2}{\sim}$ be given.
     • Suppose $\bar{f}(x)\ne\bar{f}(y)$ - then by the nature of logical implication we do not care about the RHS and are done regardless of $x$ and $y$'s equality
       • Once again I note we must really have $x\ne y$ as if $x=y$ then by definition of $\bar{f}$ being a function we must also have $\bar{f}(x)=\bar{f}(y)$, anyway!
     • Suppose that $\bar{f}(x)=\bar{f}(y)$, we must show that in this case $x=y$.
       • Note that by surjectivity of $\pi$ that: $\exists a\in D^2[\pi(a)=x]$ and $\exists b\in D^2[\pi(b)=y]$, so $\bar{f}(x)=\bar{f}(\pi(a))$ and $\bar{f}(y)=\bar{f}(\pi(b))$, also, as $\bar{f}$ was the result of factoring, we have $f=\bar{f}\circ\pi$, so we see $\bar{f}(\pi(a))=f(a)$ and $\bar{f}(\pi(b))=f(b)$, since $\bar{f}(x)=\bar{f}(y)$ we get $f(a)=f(b)$ and $\bar{f}(\pi(a))=\bar{f}(\pi(b))$ also.
         • We now have 2 cases, $a\in D^2-\partial D^2$ and $a\in \partial D^2$ respectively:
           1. Suppose $a\in D^2-\partial D^2$
              • As we have $f(a)=f(b)$ we must have $b=a$, as if $b\ne a$ then $f(b)\ne f(a)$, because $f\big\vert_{D^2-\partial D^2}:(D^2-\partial D^2)\rightarrow\mathbb{S}^2$ is injective by construction
                • If $b=a$ then $y=\pi(b)=\pi(a)=x$ so $y=x$ as required (this is easily recognised as $x=y$)
           2. Suppose $a\in\partial D^2$
              • Then to have $f(a)=f(b)$ we must have $b\in\partial D^2$
                • This means $a\sim b$, and that means $\pi(a)=\pi(b)$
                  • But $y=\pi(b)$ and $x=\pi(a)$, so we arrive at: $x=\pi(a)=\pi(b)=y$, or $x=y$, as required.

We now know $\bar{f}$ is a continuous bijection.

Noting that $D^2$ is closed and bounded we can apply the Heine–Borel theorem to show $D^2$ is compact. As $\pi:D^2\rightarrow\frac{D^2}{\sim}$ is continuous (see quotient topology for information) we can use "the image of a compact set is compact" to conclude that $\frac{D^2}{\sim}$ is compact.

A subspace of a Hausdorff space is a Hausdorff space, as $\mathbb{S}^2$ is a topological subspace of $\mathbb{R}^3$, $\mathbb{S}^2$ is Hausdorff.

We may now use the compact-to-Hausdorff theorem (as $\bar{f}$ is a bijective continuous map between a compact space to a Hausdorff space) to show that $\bar{f}$ is a homeomorphism

As we have found a homeomorphism between $\frac{D^2}{\sim}$ and $\mathbb{S}^2$ we have shown they are homeomorphic, written:

• $\frac{D^2}{\sim}\cong\mathbb{S}^2$.

Question 8

Suppose that $f:X\rightarrow Y$ is a continuous function that is also surjective, and let $\sim$ denote the equivalence relation induced by $f$ on $X$.

Show that if $X$ is compact and $Y$ is Hausdorff then $\frac{X}{\sim}$ is homeomorphic to $Y$.

Which theorem of group theory does this resemble?

Proof

Recall the result of question 5:

• "If a surjective continuous map is factored through the canonical projection of the equivalence relation induced by that map then the yielded map is a continuous bijection"

Using the linked theorem we instantly obtain:

• $\bar{f}:\frac{X}{\sim}\rightarrow Y$ that is a continuous bijection
  • We must show this is a homeomorphism.

Suppose $X$ is compact, then $\frac{X}{\sim}$ is compact also as the image of a compact set is compact and $\pi:X\rightarrow\frac{X}{\sim}$ is continuous (see quotient topology for more details)

We then apply the "compact-to-Hausdorff theorem" which shows us that $\bar{f}$ is actually a homeomorphism

This is similar to the first group isomorphism theorem (in the case the map is surjective) certainly in a categorical sense. The group theorem "factors through the kernel of the morphism" where as this "factors through the equivalence relation induced by the morphism" and they both yield an isomorphism (a homeomorphism is the term for a topological isomorphism. Here are diagrams:

• For any (surjective) group homomorphism $\varphi:G\rightarrow H$ (for arbitrary groups) we get a group isomorphism, $\bar{\varphi}$. $\xymatrix{ G \ar[r]^\varphi \ar[d]_\pi & H \\ {G/\text{Ker}(\varphi)} \ar@{.>}[ur]_{\bar{\varphi} } }$, and,
• For any (surjective) continuous map, $f:X\rightarrow Y$ (for an arbitrary compact space $X$, and arbitrary Hausdorff space $Y$) we get a homeomorphism/topological isomorphism $\bar{f}$. $\xymatrix{ X \ar[d]_\pi \ar[r]^f & Y \\ \frac{X}{x_1\sim x_2\iff f(x_1)=f(x_2)} \ar@{.>}[ur]_(.6){\bar{f} } }$

In both instances the "denominator" of the quotient depends on the map, factoring (as in passing to the quotient (function) is involved, rather than passing to the quotient (topology) and we get an isomorphism.

I hope this is the similarity that is expected.