Exercises:Mond - Topology - 2/Section B/Question 5

Section B

Question 5

Is the quotient map from [ilmath][0,1]\times[0,1]\subset\mathbb{R}^2[/ilmath] to the real projective plane, [ilmath]\mathbb{RP}^2[/ilmath], an open map?

Solution

We will consider the square as [ilmath]I^2\subset\mathbb{R}^2[/ilmath] where [ilmath]I:=[0,1]:=\{x\in\mathbb{R}\ \vert\ 0\le x\le 1\}\subset\mathbb{R}[/ilmath] with [ilmath]v_0=(0,0)[/ilmath], [ilmath]v_1=(1,0)[/ilmath], [ilmath]v_2=(0,1)[/ilmath] and [ilmath]v_3=(1,1)[/ilmath].

Definitions

We notice that for some open ball in [ilmath]I^2[/ilmath] (in green) that the image of it in [ilmath]\mathbb{RP}^2[/ilmath] under [ilmath]\pi[/ilmath] has boundary points. To show this we must show for any open neighbourhood [ilmath]U[/ilmath] (shown in red) to a suspected boundary point (which is[ilmath]\pi(v_3)=\pi(v_0)[/ilmath]) contains a point inside and a point outside the image of [ilmath]X[/ilmath] (green). To find this we use open balls in [ilmath]I^2[/ilmath] contained inside the pre-image of [ilmath]U[/ilmath] (purple) - which are open by continuity.
Notice that the diagonal which shows the image of the edges under [ilmath]\pi[/ilmath] is not straight or even smooth (shown at the extremes from [ilmath]\pi(v_3)[/ilmath]), we draw it this way for convenience!

We take the following:

• Let [ilmath]\pi:I^2\rightarrow\mathbb{RP}^2[/ilmath] be the quotient map the question talks about.
• Let [ilmath]\epsilon\in (0,\frac{\sqrt{2} }{2})\subset\mathbb{R} [/ilmath] be given, the upper bound is chosen so the open ball considered at a vertex does not cross any diagonals of the square.
• Let [ilmath]X:=B_\epsilon(v_3)\cap I^2[/ilmath], where the open ball [ilmath]B_\epsilon(v_3)[/ilmath] of radius [ilmath]\epsilon[/ilmath] centred at [ilmath]v_3[/ilmath] is considered in [ilmath]\mathbb{R}^2[/ilmath], thus [ilmath]B_\epsilon(v_3)\cap I_2[/ilmath] is open in the subspace topology [ilmath]I^2[/ilmath] inherits from [ilmath]\mathbb{R}^2[/ilmath]

Outline of solution

We will show that [ilmath]\pi[/ilmath] is not an open map, by showing that [ilmath]\pi(X)[/ilmath] has a boundary point, namely [ilmath]\pi(v_3)[/ilmath] itself and combine this with:

• A set is an open set if and only if it contains none of its boundary points

As [ilmath]\pi(X)[/ilmath] has a boundary point contained in [ilmath]\pi(X)[/ilmath] it cannot be open! We have exhibited an open set of [ilmath]I^2[/ilmath] (namely [ilmath]X[/ilmath]) which is mapped to a non-open set (namely [ilmath]\pi(X)[/ilmath]), thus [ilmath]\pi[/ilmath] cannot be an open map

Solution body

Final setup in [ilmath]I^2[/ilmath]. The colours mean: Green - [ilmath]X[/ilmath], Red - [ilmath]\pi^{-1}(U)[/ilmath] and Purple - [ilmath]\pi(B_{\delta_1}(V_0)[/ilmath] and [ilmath]\pi_{\delta_2}(v_3)[/ilmath].
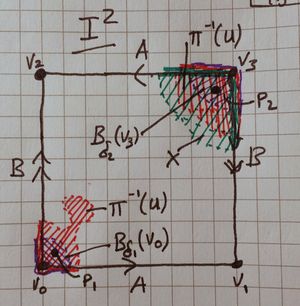
Notice that for any of the purple open balls, there is always a point ([ilmath]p_1[/ilmath] and [ilmath]p_2[/ilmath]) that is not a vertex point nor an edge point. This is key.

• Let [ilmath]\epsilon>0[/ilmath] be given such that [ilmath]\epsilon\in\mathbb{R} [/ilmath] and [ilmath]\epsilon<\frac{\sqrt{2} }{2} [/ilmath]
  • Define [ilmath]X:=B_\epsilon(v_3;\mathbb{R}^2)\cap I^2[/ilmath] - the intersection of the open ball of radius [ilmath]\epsilon[/ilmath], in [ilmath]\mathbb{R}^2[/ilmath] and [ilmath]I^2[/ilmath], by definition of the subspace topology [ilmath]X[/ilmath] is open in [ilmath]I^2[/ilmath]
    • We claim that [ilmath]\pi(v_3)\in\partial\pi(X)[/ilmath] - that is that [ilmath]\pi(v_3)[/ilmath] is a boundary point of [ilmath]\pi(X)[/ilmath].
    • To show this we will use a point is in the boundary of a set if and only if every open neighbourhood to that point contains both a point in the set and a point not in the set
      • Let [ilmath]U[/ilmath] be an arbitrary open neighbourhood in [ilmath]\mathbb{RP}^2[/ilmath] to [ilmath]\pi(v_3)[/ilmath] be given.
        • As [ilmath]\pi[/ilmath] is continuous we have [ilmath]\pi^{-1}(U)[/ilmath] is open in [ilmath]I^2[/ilmath]
        • As [ilmath]\pi(v_3)\in U[/ilmath] (by definition) and [ilmath]\pi(v_3)=\pi(v_0)[/ilmath] we see from [ilmath]\pi(v_0)\in U[/ilmath] that [ilmath]v_0\in\pi^{-1}(U)[/ilmath]
          • As [ilmath]\pi^{-1}(U)[/ilmath] is an open set and [ilmath]v_0,v_3\in\pi^{-1}(U)[/ilmath] we see there exist [ilmath]\delta_1',\delta_2'>0[/ilmath] such that [ilmath]B_{\delta_1'}(v_0)\subset\pi^{-1}(U)[/ilmath] and [ilmath]B_{\delta_2'}(v_3)\subset\pi^{-1}(U)[/ilmath]
          • Define [ilmath]\delta_1:=\text{Max}(\{\delta_1',\frac{\sqrt{2} }{2}\})[/ilmath] and [ilmath]\delta_1:=\text{Max}(\{\delta_1',\frac{\sqrt{2} }{2}\})[/ilmath] - this will prevent the following balls from crossing the diagonal of the square and keeps them disjoint.
          • Notice the following: [ilmath]B_{\delta_1}(v_0)\subseteq B_{\delta_1'}(v_0)\subset \pi^{-1}(U)[/ilmath] and [ilmath]B_{\delta_2}(v_3)\subseteq B_{\delta_2'}(v_3)\subset \pi^{-1}(U)[/ilmath]
            • Define [ilmath]p_1\in B_{\delta_1}(v_0)[/ilmath] to be any point in [ilmath]B_{\delta_1}(v_0)[/ilmath] such that [ilmath]p_1\ne v_0[/ilmath] and both the [ilmath]x[/ilmath] and [ilmath]y[/ilmath] coordinates are not [ilmath]0[/ilmath] (for example: [ilmath]p_1:=(\frac{\delta_1}{2},\frac{\delta_1}{2})[/ilmath] would do nicely)
            • Define [ilmath]p_2\in B_{\delta_2}(v_3)[/ilmath] to be any point in [ilmath]B_{\delta_2}(v_3)[/ilmath] such that [ilmath]p_2\ne v_3[/ilmath] and both the [ilmath]x[/ilmath] and [ilmath]y[/ilmath] coordinates are not [ilmath]1[/ilmath] (for example: [ilmath]p_2:=(1-\frac{\delta_2}{2},1-\frac{\delta_2}{2})[/ilmath] would do nicely)
              

              Notice that [ilmath]\pi(p_2)[/ilmath] is inside the image of [ilmath]X[/ilmath] (green) and inside [ilmath]U[/ilmath], then contrast that with [ilmath]\pi(p_1)[/ilmath] which is not inside the image of [ilmath]X[/ilmath]. Purple shows the image of the open balls at each vertex, which we used to obtain [ilmath]p_1[/ilmath] and [ilmath]p_2[/ilmath]
              • Notice: The situation is shown in the 3^rd diagram on the right
                1. [ilmath]\pi(p_1)\in U[/ilmath] and [ilmath]\pi(p_2)\in U[/ilmath]
                2. [ilmath]\pi(p_2)\in\pi(X)[/ilmath]
                3. [ilmath]\pi(p_1)\notin\pi(X)[/ilmath]
                4. [ilmath]\pi(p_1)\neq \pi(v_3)[/ilmath] and
                5. [ilmath]\pi(p_2)\neq \pi(v_1)[/ilmath] It my be unnecessary to find a point distinct from the (suspected) boundary point inside and outside of [ilmath]X[/ilmath], however as it was only a minor detour, we have done it
                   • Note that [ilmath]\pi[/ilmath] restricted to [ilmath](0,1)\times(0,1)[/ilmath] (the interior of the [ilmath]I^2[/ilmath] considered in the space [ilmath]\mathbb{R}^2[/ilmath]) is injective so we see [ilmath]\pi(p_1)\ne\pi(p_2)[/ilmath]
                   • Next, observe that (by design, this is the whole point of identification spaces like this) the edges by each point are mapped over each other (in direction depending on the arrows in the identification), as [ilmath]p_1[/ilmath] and [ilmath]p_2[/ilmath] are not on the edge, nor are they vertices, they are not mapped to it.
              • So now we have: [ilmath]\pi(p_1)\in U[/ilmath], [ilmath]\pi(p_2)\in U[/ilmath] and importantly, for the boundary point theorem mentioned above:
                • [ilmath]\pi(p_1)\notin\pi(X)[/ilmath] and [ilmath]\pi(p_2)\in\pi(X)[/ilmath]
      • Since our choice of [ilmath]U[/ilmath] (an open neighbourhood to [ilmath]\pi(v_3)[/ilmath]) was arbitrary, we have shown for all such [ilmath]U[/ilmath] there exists points inside of [ilmath]U[/ilmath] such that 1 is inside [ilmath]\pi(X)[/ilmath] and one is outside [ilmath]\pi(X)[/ilmath]; namely [ilmath]\pi(p_1)[/ilmath] and [ilmath]\pi(p_2)[/ilmath].
        • We actually went a bit to far and found a point in the interior of [ilmath]\pi(X)[/ilmath]
    • We apply the theorem: "a point is in the boundary of a set if and only if every open neighbourhood to that point contains both a point in the set and a point not in the set" to show:
      • [ilmath]\pi(v_3)\in\partial(\pi(X))[/ilmath] (where [ilmath]\partial A[/ilmath] denotes the boundary of a set [ilmath]A[/ilmath] in some topological space)
    • Next, we recall the theorem: "a set is an open set if and only if it contains none of its boundary points"
    • Well, [ilmath]\pi(v_3)\in\partial(\pi(X))[/ilmath] so [ilmath]\pi(X)[/ilmath] contains (at least) 1 of its boundary points, therefore it cannot be open.
    • As [ilmath]X\subset I^2[/ilmath] is open, but its image, [ilmath]\pi(X)\subset\mathbb{RP}^2[/ilmath] is not open, [ilmath]\pi[/ilmath] cannot be an open map, as:
      • To be an open map, the image of every open set in the domain ([ilmath]I^2[/ilmath]) must be open in [ilmath]\mathbb{RP}^2[/ilmath], we have demonstrated this is not the case

Thus [ilmath]\pi[/ilmath] is not an open map.