Exercises:Mond - Topology - 2/Section B/Question 8

Section B

Question 8

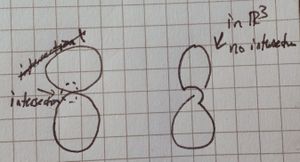
Here is a proof that the Klein bottle can be topologically embedded in $\mathbb{R}^4$. The drawing on the right below shows the image of a failed embedding of the Klein bottle in $\mathbb{R}^3$, $f:K\rightarrow\mathbb{R}^3$. The surface has to pass through itself in order for the two ends of the cylinder to glue together as required.

To embed $K$ in $\mathbb{R}^4$ the map $f$ needs one further component, $f_4:K\rightarrow\mathbb{R}$. You can describe $f_4$ by specifying its value at each point of $K$. By taking care that $f_4$ distinguishes points on $K$ which have the same image under $f$ in $\mathbb{R}^3$ (i.e. in the picture), you obtain an embedding. Copy the right hand picture and write suitable values of $f_4$ on your copy. Your $f_4$ should be continuous.

Solution

My preferred form

What is probably wanted

The idea here is that I use a green line's thickness to denote the value of $f_4$, and assume it is 0 unless specified. In this image we associate the thinner "component" (I do not want to invoke a formal definition) of the bottle with the green line shown inside of it, and we show the bulb-like component with a line representing $f_4=0$. The idea is we "lift" the smaller component over the bulb where they would otherwise intersect, then lower it back down afterwards.

I sense this is the kind of thing that you're after (Mond, my tutor, has drawn a diagram like this before). We assign 0 to everything, and as the thinner component comes to intersect the "bulb", we raise it, continuously, which I've tried to convey by first raising from $0$ to $\frac{1}{2}$ then $1$ then back down to $\frac{1}{2}$ then 0. The blue line is intended to convey the bulb stays at $f_4=0$

Lower dimensional analogy

Forgive the badly-drawn-ness of this image, I apologise profusely for my inability to judge the length of the word "intersection" not once but twice.

I want to convey understanding. This is a very similar lower-dimensional analogy, we have the figure-8 / $\infty$ space, and we want to make it into an embedding in $\mathbb{R}^3$. To do this we first take the $\infty$ flat into $\mathbb{R}^3$ then pick one of the components of the line (it doesn't matter which) and in a small area alter it's new coordinate so it goes "over" where it'd otherwise intersect.