Exercises:Mond - Topology - 1/Question 7

Section B

Question 7

Let [ilmath]D^2[/ilmath] denote the closed unit disk in [ilmath]\mathbb{R}^2[/ilmath] and define an equivalence relation on [ilmath]D^2[/ilmath] by setting [ilmath]x_1\sim x_2[/ilmath] if [ilmath]\Vert x_1\Vert=\Vert x_2\Vert=1[/ilmath] ("collapsing the boundary to a single point"). Show that [ilmath]\frac{D^2}{\sim} [/ilmath] is homeomorphic to [ilmath]\mathbb{S}^2[/ilmath] - the sphere.

• Hint: first define a surjection [ilmath](:D^2\rightarrow\mathbb{S}^2)[/ilmath] mapping all of [ilmath]\partial D^2[/ilmath] to the north pole. This may be defined using a good picture or a formula.

Solution

The idea is to double the radius of [ilmath]D^2[/ilmath], then pop it out into a hemisphere, then pull the rim to a point

Picture showing the "expanding [ilmath]D^2[/ilmath]", the embedding-in-[ilmath]\mathbb{R}^3[/ilmath] part, and the "popping out"

Definitions:

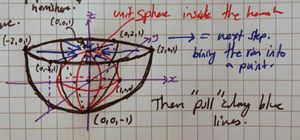
• [ilmath]H[/ilmath] denotes the hemisphere in my picture.
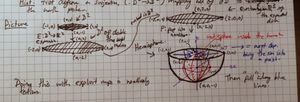
• [ilmath]E:D^2\rightarrow H[/ilmath] is the composition of maps in my diagram that take [ilmath]D^2[/ilmath], double its radius, then embed it in [ilmath]\mathbb{R}^3[/ilmath] then "pop it out" into a hemisphere. We take it as obvious that it is a homeomorphism
• [ilmath]f':H\rightarrow\mathbb{S}^2[/ilmath], this is the map in the top picture. It takes the hemisphere and pulls the boundary/rim in (along the blue lines) to the north pole of the red sphere. [ilmath]f'(\partial H)=(0,0,1)\in\mathbb{R}^3[/ilmath], it should be clear that for all [ilmath]x\in H-\partial H[/ilmath] that [ilmath]f'(x)[/ilmath] is intended to be a point on the red sphere and that [ilmath]f'\big\vert_{H-\partial H}[/ilmath] is injective. It is also taken as clear that [ilmath]f'[/ilmath] is surjective
• Note: Click the pictures for a larger version
• [ilmath]\frac{D^2}{\sim} [/ilmath] and [ilmath]D^2/\sim[/ilmath] denote the quotient space, with this definition we get a canonical projection, [ilmath]\pi:D^2\rightarrow D^2/\sim[/ilmath] given by [ilmath]\pi:x\mapsto [x][/ilmath] where [ilmath][x][/ilmath] denotes the equivalence class of [ilmath]x[/ilmath]
• Lastly, we define [ilmath]f:D^2\rightarrow\mathbb{S}^2[/ilmath] to be the composition of [ilmath]E[/ilmath] and [ilmath]f'[/ilmath], that is: [ilmath]f:=f'\circ E[/ilmath], meaning [ilmath]f:x\mapsto f'(E(x))[/ilmath]

The situation is shown diagramatically below:

• [ilmath]\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f:=f'\circ E} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} }[/ilmath]

Outline of the solution:

• We then want apply the passing to the quotient theorem to yield a commutative diagram: [ilmath]\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} \ar@{.>}[urr]_{\bar{f} } }[/ilmath]
  • The commutative diagram part merely means that [ilmath]f=\bar{f}\circ\pi[/ilmath]. We get [ilmath]f=\bar{f}\circ\pi[/ilmath] as a result of the passing-to-the-quotient theorem.
  • We take this diagram as showing morphisms in the TOP category, meaning all arrows shown represent continuous maps. (Obviously...)
• Lastly, we will show that [ilmath]\bar{f} [/ilmath] is a homeomorphism using the compact-to-Hausdorff theorem

Solution body

First we must show the requirements for applying passing to the quotient are satisfied.

• We know already the maps involved are continuous and that [ilmath]\pi[/ilmath] is a quotient map. We only need to show:
  • [ilmath]f[/ilmath] is constant on the fibres of [ilmath]\pi[/ilmath], which is equivalent to:
    • [ilmath]\forall x,y\in D^2[\pi(x)=\pi(y)\implies f(x)=f(y)][/ilmath]
• Let us show this remaining condition:
  • Let [ilmath]x,y\in D^2[/ilmath] be given.
    • Suppose [ilmath]\pi(x)\ne\pi(y)[/ilmath], then by the nature of logical implication the implication is true regardless of [ilmath]f(x)[/ilmath] and [ilmath]f(y)[/ilmath]'s equality. We're done in this case.
    • Suppose [ilmath]\pi(x)=\pi(y)[/ilmath], we must show that in this case [ilmath]f(x)=y(y)[/ilmath].
      • Suppose [ilmath]x\in D^2-\partial D^2[/ilmath] (meaning [ilmath]x\in D^2[/ilmath] but [ilmath]x\notin \partial D^2[/ilmath], ie [ilmath]-[/ilmath] denotes relative complement)
        • In this case we must have [ilmath]x=y[/ilmath], as otherwise we'd not have [ilmath]\pi(x)=\pi(y)[/ilmath] (for [ilmath]x\in D^2-\partial D^2[/ilmath] we have [ilmath]\pi(x)=[x]=\{x\}[/ilmath], that is that the equivalence classes are singletons. So if [ilmath]\pi(x)=\pi(y)[/ilmath] we must have [ilmath]\pi(y)=[y]=\{x\}=[x]=\pi(x)[/ilmath]; so [ilmath]y[/ilmath] can only be [ilmath]x[/ilmath])
        • If [ilmath]x=y[/ilmath] then by the nature of [ilmath]f[/ilmath] being a function we must have [ilmath]f(x)=f(y)[/ilmath], we're done in this case
      • Suppose [ilmath]x\in \partial D^2[/ilmath] (the only case not covered) and [ilmath]\pi(x)=\pi(y)[/ilmath], we must show [ilmath]f(x)=f(y)[/ilmath]
        • Clearly if [ilmath]x\in\partial D^2[/ilmath] and [ilmath]\pi(x)=\pi(y)[/ilmath] we must have [ilmath]y\in\partial D^2[/ilmath].
          • [ilmath]E(x)[/ilmath] is mapped to the boundary/rim of [ilmath]H[/ilmath], as is [ilmath]E(y)[/ilmath] and [ilmath]f'(\text{any point on the rim of }H)=(0,0,1)\in\mathbb{R}^3[/ilmath]
          • Thus [ilmath]f'(E(x))=f'(E(y))[/ilmath], but [ilmath]f'(E(x))[/ilmath] is the very definition of [ilmath]f(x)[/ilmath], so clearly:
            • [ilmath]f(x)=f(y)[/ilmath] as required.

We may now apply the passing to the quotient theorem. This yields:

• A continuous map, [ilmath]\bar{f}:D^2/\sim\rightarrow\mathbb{S}^2[/ilmath] where [ilmath]f=\bar{f}\circ\pi[/ilmath]

[ilmath]\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} \ar@{.>}[urr]_{\bar{f} } }[/ilmath]
Commutative diagram of situation (all maps are continuous)

We now have the situation of the diagram on the right, restated from above for convenience.

In order to apply the compact-to-Hausdorff theorem and show [ilmath]\bar{f} [/ilmath] is a homeomorphism we must show it is continuous and bijective. We already have continuity (as a result of the passing-to-the-quotient theorem), we must show it is bijective.

We must show [ilmath]\bar{f} [/ilmath] is both surjective and injective:

1. Surjectivity: We can get this from the definition of [ilmath]\bar{f} [/ilmath], recall on the passing to the quotient (function) page that:
   • if [ilmath]f[/ilmath] is surjective then [ilmath]\bar{f} [/ilmath] (or [ilmath]\tilde{f} [/ilmath] as the induced function is on that page) is surjective also
     • I've already done it "the long way" once in this assignment, and I hope it is not frowned upon if I decline to do it again.
2. Injectivity: This follows a similar to gist as to what we've done already to show we could apply "passing to the quotient" and for the other questions where we've had to show a factored map is injective. As before:
   • Let [ilmath]x,y\in\frac{D^2}{\sim} [/ilmath] be given.
     • Suppose [ilmath]\bar{f}(x)\ne\bar{f}(y)[/ilmath] - then by the nature of logical implication we do not care about the RHS and are done regardless of [ilmath]x[/ilmath] and [ilmath]y[/ilmath]'s equality
       • Once again I note we must really have [ilmath]x\ne y[/ilmath] as if [ilmath]x=y[/ilmath] then by definition of [ilmath]\bar{f} [/ilmath] being a function we must also have [ilmath]\bar{f}(x)=\bar{f}(y)[/ilmath], anyway!
     • Suppose that [ilmath]\bar{f}(x)=\bar{f}(y)[/ilmath], we must show that in this case [ilmath]x=y[/ilmath].
       • Note that by surjectivity of [ilmath]\pi[/ilmath] that: [ilmath]\exists a\in D^2[\pi(a)=x][/ilmath] and [ilmath]\exists b\in D^2[\pi(b)=y][/ilmath], so [ilmath]\bar{f}(x)=\bar{f}(\pi(a))[/ilmath] and [ilmath]\bar{f}(y)=\bar{f}(\pi(b))[/ilmath], also, as [ilmath]\bar{f} [/ilmath] was the result of factoring, we have [ilmath]f=\bar{f}\circ\pi[/ilmath], so we see [ilmath]\bar{f}(\pi(a))=f(a)[/ilmath] and [ilmath]\bar{f}(\pi(b))=f(b)[/ilmath], since [ilmath]\bar{f}(x)=\bar{f}(y)[/ilmath] we get [ilmath]f(a)=f(b)[/ilmath] and [ilmath]\bar{f}(\pi(a))=\bar{f}(\pi(b))[/ilmath] also.
         • We now have 2 cases, [ilmath]a\in D^2-\partial D^2[/ilmath] and [ilmath]a\in \partial D^2[/ilmath] respectively:
           1. Suppose [ilmath]a\in D^2-\partial D^2[/ilmath]
              • As we have [ilmath]f(a)=f(b)[/ilmath] we must have [ilmath]b=a[/ilmath], as if [ilmath]b\ne a[/ilmath] then [ilmath]f(b)\ne f(a)[/ilmath], because [ilmath]f\big\vert_{D^2-\partial D^2}:(D^2-\partial D^2)\rightarrow\mathbb{S}^2[/ilmath] is injective by construction
                • If [ilmath]b=a[/ilmath] then [ilmath]y=\pi(b)=\pi(a)=x[/ilmath] so [ilmath]y=x[/ilmath] as required (this is easily recognised as [ilmath]x=y[/ilmath])
           2. Suppose [ilmath]a\in\partial D^2[/ilmath]
              • Then to have [ilmath]f(a)=f(b)[/ilmath] we must have [ilmath]b\in\partial D^2[/ilmath]
                • This means [ilmath]a\sim b[/ilmath], and that means [ilmath]\pi(a)=\pi(b)[/ilmath]
                  • But [ilmath]y=\pi(b)[/ilmath] and [ilmath]x=\pi(a)[/ilmath], so we arrive at: [ilmath]x=\pi(a)=\pi(b)=y[/ilmath], or [ilmath]x=y[/ilmath], as required.

We now know [ilmath]\bar{f} [/ilmath] is a continuous bijection.

Noting that [ilmath]D^2[/ilmath] is closed and bounded we can apply the Heine–Borel theorem to show [ilmath]D^2[/ilmath] is compact. As [ilmath]\pi:D^2\rightarrow\frac{D^2}{\sim} [/ilmath] is continuous (see quotient topology for information) we can use "the image of a compact set is compact" to conclude that [ilmath]\frac{D^2}{\sim} [/ilmath] is compact.

A subspace of a Hausdorff space is a Hausdorff space, as [ilmath]\mathbb{S}^2[/ilmath] is a topological subspace of [ilmath]\mathbb{R}^3[/ilmath], [ilmath]\mathbb{S}^2[/ilmath] is Hausdorff.

We may now use the compact-to-Hausdorff theorem (as [ilmath]\bar{f} [/ilmath] is a bijective continuous map between a compact space to a Hausdorff space) to show that [ilmath]\bar{f} [/ilmath] is a homeomorphism

As we have found a homeomorphism between [ilmath]\frac{D^2}{\sim} [/ilmath] and [ilmath]\mathbb{S}^2[/ilmath] we have shown they are homeomorphic, written:

• [ilmath]\frac{D^2}{\sim}\cong\mathbb{S}^2[/ilmath].