Exercises:Mond - Topology - 2/Section B/Question 7

Section B

Question 7

Both the Klein bottle and the real projective plane are [ilmath]2[/ilmath]-manifolds. This is not obvious from their descriptions as quotients of the square by an equivalence relation. In fact each point [ilmath]x[/ilmath] does have an open neighbourhood homeomorphic to an open set in [ilmath]\mathbb{R}^2[/ilmath]. Show by carefully labelled drawings that this is true if:

1. [ilmath]x[/ilmath] is in the image of the interior of the square.
   • Caution:Mond VERY PROBABLY ALMOST CERTAINLY means the interior of the square considered as a set in [ilmath]\mathbb{R}^2[/ilmath], as of course the square's interior is itself when considered as a topological subspace
2. [ilmath]x[/ilmath] is in the image of an edge in the square, but not of a vertex.
3. [ilmath]x[/ilmath] is the image of a vertex.

Your drawings for 2 and 3 have to make use of the fact that the edges of the square are glue together in passing to the quotient.

Solution

Definitions

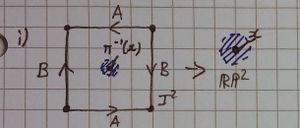
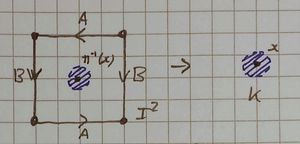
We take the following diagrams as the "square-edge-gluing" (identification?) diagrams used:

The Klein bottle	[ilmath]\mathbb{RP}^2[/ilmath]
[ilmath]\xymatrix{ \bullet \ar@{<-}[r]^A \ar[d]_B & \bullet \ar[d]^B \\ \bullet \ar@{->}[r]_A & \bullet }[/ilmath]	[ilmath]\xymatrix{ \bullet \ar@{<-}[r]^A \ar@{<-}[d]_B & \bullet \ar[d]^B \\ \bullet \ar@{->}[r]_A & \bullet }[/ilmath]

Solution body

Notice this is [ilmath]\mathbb{RP}^2[/ilmath] in the first column. Pictures have comments underneath.

• To see these in a table rather than as separate images see Media:TableSourceForLocallyKbottleAndRP2.JPG

The work here is done very informally. I emailed a link to: Media:RP2locallyDraft.JPG and was told this was the right idea.

Type	[ilmath]\mathbb{RP}^2[/ilmath]	Klein bottle
Case [ilmath]1[/ilmath]
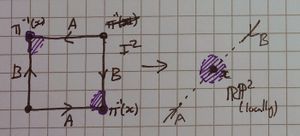
	these cases are self explanatory and trivial, for any point in the interior of the square (considered in [ilmath]\mathbb{R}^2[/ilmath]) [ilmath]\pi[/ilmath] is injective (in fact [ilmath]\pi[/ilmath] restricted to the interior of the square (considered in [ilmath]\mathbb{R}^2[/ilmath]) is a homeomorphism onto its image), this can be used to show that given any such [ilmath]x[/ilmath] there is an open ball around [ilmath]x[/ilmath] which does not touch any edges or vertices of the square, or their images.
Case [ilmath]2[/ilmath]
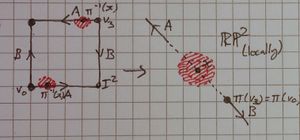
	The other cases are essentially the same just with the nearest vertex (marked here as [ilmath]\pi(v_0)=\pi(v_3)[/ilmath]) on the other side, or the arrows going another direction.	The other cases are just as in the already shown [ilmath]\mathbb{RP}^2[/ilmath] case, possibly with arrows in a different direction, or the nearest vertex on the other side.
	To be explicit, notice the edges in the square have a red border where the red open sets are, this is to convey the edges are in that set. The passing to the quotient operation will map the edges onto each other, gluing the red set together along it, in the direction of the arrow on that edge. What we are really showing here is an open ball in the chart, centred at [ilmath]x[/ilmath] and it's pre-image in the chart, then that's pre-image under the quotient map (in the square) This comment also applies to the third case.
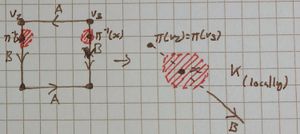
Case [ilmath]3[/ilmath]		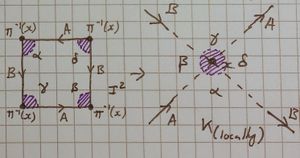there's a slight mistake in this diagram, notice that all the other diagrams have a border around the exterior of the square to denote that they include that part of the edge, or that vertex, they should be present here. That is all the purple sections should include the edge they touch as well as the vertex. Please imagine them in.
	The other case is essentially the same just with the arrow directions reversed.	There is no other case. I have put [ilmath]\alpha,\beta,\gamma[/ilmath] and [ilmath]\delta[/ilmath] in each quadrant to show which shaded in bit belongs to which