Exercises:Mond - Topology - 2/Section B/Question 6

Section B

Question 6

[ilmath]M[/ilmath] is a Mobius strip inside [ilmath]\mathbb{RP}^2[/ilmath]
[ilmath]\xymatrix{ \bullet \ar@{<-}[dd]_B \ar@{<.}@/^1em/[rrr]^{(A)} \ar@{<-}[r]_{A_1} & \bullet \ar@{<-}[r]_{A_2} \ar@{}[ddr]\|(.5){\mathbf{M} } \ar@{-->}@/_.65em/[dd]^{C_1} \ar@{-->}@/^.65em/[dd] & \bullet \ar@{<-}[r]_{A_3} \ar@{-->}@/_.65em/[dd]^{C_2} \ar@{-->}@/^.65em/[dd] & \bullet \\ & & &\\ \bullet \ar@{.>}@/_1em/[rrr]_{(A)} \ar[r]^{A_3} & \bullet \ar[r]^{A_2} & \bullet \ar[r]^{A_1} & \bullet \ar@{<-}[uu]_B }[/ilmath] We take [ilmath]\mathbb{RP}^2[/ilmath] (represented here as the gluings [ilmath]A[/ilmath] and [ilmath]B[/ilmath]) and cut it (creating gluings [ilmath]C_1[/ilmath] and [ilmath]C_2[/ilmath]), thus diving [ilmath]A[/ilmath] into [ilmath]A_1[/ilmath], [ilmath]A_2[/ilmath] and [ilmath]A_3[/ilmath]. The central strip is called [ilmath]M[/ilmath]

The picture on the right shows that [ilmath]\mathbb{RP}^2[/ilmath] contains a Mobius strip, [ilmath]M[/ilmath]. Use the diagram, taking into account the glueings, to describe the complement of [ilmath]M[/ilmath] in [ilmath]\mathbb{RP}^2[/ilmath]. You mare allowed to cut it, provided you then glue it back together.

Complete the following sentence in as clear a way as possible:

"[ilmath]\mathbb{RP}^2[/ilmath] is obtained from a Mobius strip by ....."

Solution

I only claim to find a topological immersion - the result is not a homeomorphism as it isn't a bijection.

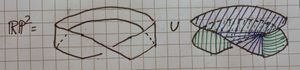
This picture belongs to my solution

Result. The "dog-bone-disk" structure we construct is on the right, blue is the top disk and green the lower. We then align it up and "union" it with the Mobius band to obtain a topological immersion of [ilmath]\mathbb{RP}^2[/ilmath]

The steps are:

Create the Mobius band and put it aside for the moment, call it [ilmath]M[/ilmath].
Take a disk. Call it [ilmath]N[/ilmath]. This is shown in the picture on the right
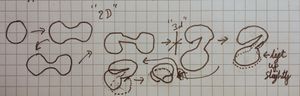
1. Stretch the disk slightly, the goal is to create something that resembles two disks joined, but not joined at a point. If you were to take a small "sausage" of blu-tac, and pinch the edges you'd end up with 2 disks joined by a strip of blu-tac, we want this. This is shown in the first 3 stages of the series on the right.
  - Caution:We do not want, nor do we mean, two circles joined at a point (see: wedge product)
2. We cut in the edges slightly, so we no longer have two disks, but rather cut in disk with a rectangle coming off it. This is hard to describe and shown in stage 4 in the series on the right
3. We now (topologically) embed the resulting shape in [ilmath]\mathbb{R}^3[/ilmath] (rather than the plane, [ilmath]\mathbb{R}^2[/ilmath]) - shown in stage 5
4. Looking at the "cut in" disk furtherest away from the observer in my drawing, we look at the line which (if drawn) would mark the disk's edge and the rectangle that connects the disks start. We take that line and we rotate it [ilmath]90^\circ[/ilmath] around the depth axis, so it is vertical, and perpendicular to the disks. We also raise the nearest-the-observer-disk by a height which is the height of the Mobius Band [ilmath]M[/ilmath]. This is shown in step 6.
  - The "rectangle" joining the two is now distorted by a twist along it.
5. We now start to move the upper disk over the lower disk, as we do so we rotate it to keep the distorted rectangle between them as in-alignment as we can. This is shown in step 7
6. Lastly, and by step 8 we have moved-and-rotated the upper disk over the lower. By preserving the rectangle as best we can there is automatically an "inner edge" that is shown passing behind and through into the "top" disk. Hopefully we have created the right hand side of the second picture:
  - Blue represents the top disk
  - Green represents the bottom disk
Position the result "inside" the cylinder that bounds the mobius strip
Make any minor adjustments, so that the boundary of the band and the "double-disk-twisted-back-thing" we have made can be trivially stitched together, so trivially that the result is a union operation.
It is now trivial to "stitch" the edges together. (As shown in the second picture on the right)

The workings below are more detailed and formal. I have not drawn a picture of [ilmath]\mathbb{RP}^2[/ilmath] immersed in this way for two reasons:

The picture was extremely messy and not useful if I showed both disks and the "twist" of the rectangle between them
The picture looked like a cylinder with a twist in the wall if I just drew the "top" of it and the Mobius band.

I hope it doesn't seem like a cop out to say:

I actually really like my union drawing, it is surprisingly clear.

Solution workings

Step	Picture	Comment
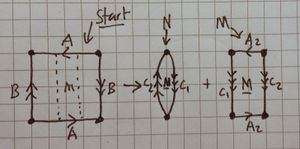
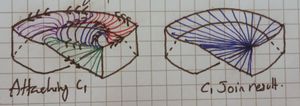
1 Dividing up the square	We first take the square and cut it up, creating new edges for gluing, [ilmath]C_1[/ilmath] and [ilmath]C_2[/ilmath] (see the picture at the top of this question)	We do this then this To yield two "chunks", [ilmath]N[/ilmath] and [ilmath]M[/ilmath].
2 Making the Mobius band	We start with [ilmath]M[/ilmath] on the left.	Pretty self explanatory and routine, my pictures turned out really well, I am a little bit proud.
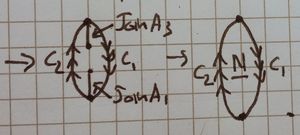
3 Joining the [ilmath]C_2[/ilmath] edges	we start off with the red, pulling the C2 edge between [ilmath]v_1[/ilmath] and [ilmath]v_2[/ilmath] part way around the [ilmath]C_2[/ilmath] edge of the band, then we let it return to [ilmath]v_1[/ilmath], [ilmath]v_1[/ilmath] and [ilmath]v_2[/ilmath] are added only for clarity. The next stage is purple, we stitch more of the edge along the [ilmath]C_2[/ilmath] edge of the band, then: Into blue, we pull it almost all the way round back to [ilmath]v_1[/ilmath]. Here the sum of the previous step is in green. 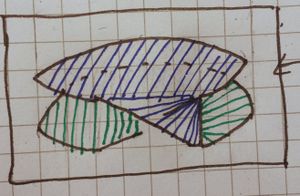We then pull the free edge inwards (red) until only a tiny amount of almost parallel [ilmath]C_2[/ilmath] join is left to do	this is the result The picture here shows only "half" of the [ilmath]N[/ilmath] surface, it is the result of stitching along the [ilmath]C_2[/ilmath] boundary.]]
4 Joining the [ilmath]C_1[/ilmath] edge	We start with the green and just pull the [ilmath]C_1[/ilmath] edge along and start stitching. Then we pull that around - and stitch along the way - resulting in purple. Then we pull that almost all the way around yielding red. As before, we then pull the free-edge in, until there's a tiny gap and the remaining join results in almost parallel curves. The right hand image shows the result, which is significantly simpler than the [ilmath]C_2[/ilmath] case
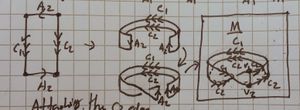
5 [ilmath]N[/ilmath] surface		This shows what becomes of [ilmath]N[/ilmath] when it is stitched to [ilmath]M[/ilmath] along the [ilmath]C_1[/ilmath] and [ilmath]C_2[/ilmath] boundaries shown earlier, without [ilmath]M[/ilmath] drawn.
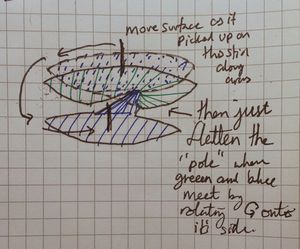
6 Final topological immersion		A diagram showing them together is very cluttered and hard to see (it either looks a mess, or a cylinder with a twist in the side), so I will show it like this. We see (a topological immersion) of [ilmath]\mathbb{RP}^2[/ilmath] in [ilmath]\mathbb{R}^3[/ilmath] is simply the union of a Möbius strip together with a "solid 8" shape, oo but joined. Take the left "disk" in this formation and lift it, then rotate it over the first disk in the formation. Showing [ilmath]N[/ilmath] is the joined oo I speak of. In this picture we imagine sticking a "stick" into the centre of the blue disk, on which the blue "wheel" can rotate freely, we move that stick along the arrows shown, the result is blue-and-green joined along a vertical pole. If you rotate that "pole" anticlockwise, so onto it's side, parallel to the x-axis on the paper it is drawn, you then have a [ilmath]oo[/ilmath] shape where the [ilmath]o[/ilmath]s are joined (that "pole" being the join between the two)