Exercises:Mond - Topology - 2/Section B/Question 7

Section B

Question 7

Both the Klein bottle and the real projective plane are $2$-manifolds. This is not obvious from their descriptions as quotients of the square by an equivalence relation. In fact each point $x$ does have an open neighbourhood homeomorphic to an open set in $\mathbb{R}^2$. Show by carefully labelled drawings that this is true if:

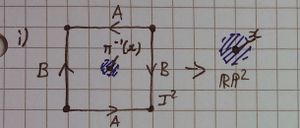
1. $x$ is in the image of the interior of the square.
   • Caution:Mond VERY PROBABLY ALMOST CERTAINLY means the interior of the square considered as a set in $\mathbb{R}^2$, as of course the square's interior is itself when considered as a topological subspace
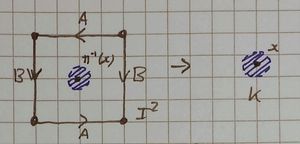
2. $x$ is in the image of an edge in the square, but not of a vertex.
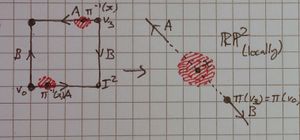
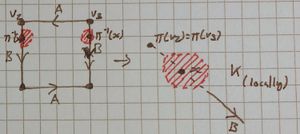
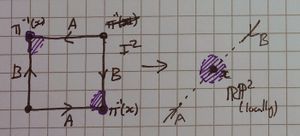
3. $x$ is the image of a vertex.

Your drawings for 2 and 3 have to make use of the fact that the edges of the square are glue together in passing to the quotient.

Solution

Definitions

We take the following diagrams as the "square-edge-gluing" (identification?) diagrams used:

The Klein bottle	$\mathbb{RP}^2$
$\xymatrix{ \bullet \ar@{<-}[r]^A \ar[d]_B & \bullet \ar[d]^B \\ \bullet \ar@{->}[r]_A & \bullet }$	$\xymatrix{ \bullet \ar@{<-}[r]^A \ar@{<-}[d]_B & \bullet \ar[d]^B \\ \bullet \ar@{->}[r]_A & \bullet }$

Solution body

Notice this is $\mathbb{RP}^2$ in the first column. Pictures have comments underneath.

• To see these in a table rather than as separate images see Media:TableSourceForLocallyKbottleAndRP2.JPG

---

TODO: Explain what is going on

---

Type	$\mathbb{RP}^2$	Klein bottle
Case $1$
Case $2$
	The other cases are essentially the same just with the nearest vertex (marked here as $\pi(v_0)=\pi(v_3)$) on the other side, or the arrows going another direction.	The other cases are just as in the already shown $\mathbb{RP}^2$ case, possibly with arrows in a different direction, or the nearest vertex on the other side.
Case $3$
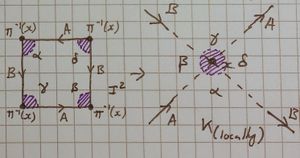
	The other case is essentially the same just with the arrow directions reversed	There is no other case. I have put $\alpha,\beta,\gamma$ and $\delta$ in each quadrant to show which shaded in bit belongs to which