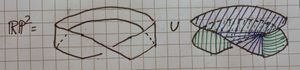Exercises:Mond - Topology - 2/Section B/Question 6

Section B

Question 6

$M$ is a Mobius strip inside $\mathbb{RP}^2$
$\xymatrix{ \bullet \ar@{<-}[dd]_B \ar@{<.}@/^1em/[rrr]^{(A)} \ar@{<-}[r]_{A_1} & \bullet \ar@{<-}[r]_{A_2} \ar@{}[ddr]\|(.5){\mathbf{M} } \ar@{-->}@/_.65em/[dd]^{C_1} \ar@{-->}@/^.65em/[dd] & \bullet \ar@{<-}[r]_{A_3} \ar@{-->}@/_.65em/[dd]^{C_2} \ar@{-->}@/^.65em/[dd] & \bullet \\ & & &\\ \bullet \ar@{.>}@/_1em/[rrr]_{(A)} \ar[r]^{A_3} & \bullet \ar[r]^{A_2} & \bullet \ar[r]^{A_1} & \bullet \ar@{<-}[uu]_B }$ We take $\mathbb{RP}^2$ (represented here as the gluings $A$ and $B$ ) and cut it (creating gluings $C_1$ and $C_2$ ), thus diving $A$ into $A_1$ , $A_2$ and $A_3$ . The central strip is called $M$

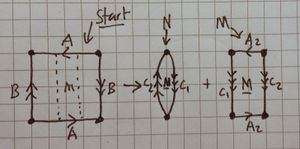
The picture on the right shows that

$\mathbb{RP}^2$ contains a Mobius strip,

$M$ . Use the diagram, taking into account the glueings, to describe the complement of

$M$ in

$\mathbb{RP}^2$ . You mare allowed to cut it, provided you then glue it back together.

Complete the following sentence in as clear a way as possible:

" $\mathbb{RP}^2$ is obtained from a Mobius strip by ....."

Solution

Step	Picture	Comment
1 Dividing up the square	We first take the square and cut it up, creating new edges for gluing, $C_1$ and $C_2$ (see the picture at the top of this question)	We do this then this To yield two "chunks", $N$ and $M$ .
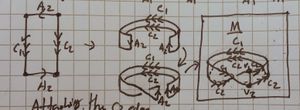
2 Making the Mobius band	We start with $M$ on the left.	Pretty self explanatory and routine, my pictures turned out really well, I am a little bit proud.
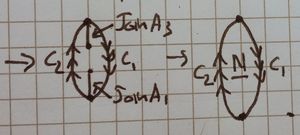
3 Joining the $C_2$ edges	v_2} part way around the $C_2$ edge of the band, then we let it return to $v_1$ , $v_1$ and $v_2$ are added only for clarity. The next stage is purple, we stitch more of the edge along the $C_2$ edge of the band, then: Into blue, we pull it almost all the way round back to $v_1$ . Here the sum of the previous step is in green. We then pull the free edge inwards (red) until only a tiny amount of almost parallel $C_2$ join is left to do	this is the result The picture here shows only "half" of the $N$ surface, it is the result of stitching along the $C_2$ boundary.]]
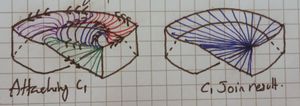
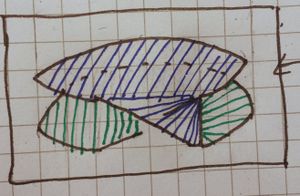
4 Joining the $C_1$ edge	We start with the green and just pull the $C_1$ edge along and start stitching. Then we pull that around - and stitch along the way - resulting in purple. Then we pull that almost all the way around yielding red. As before, we then pull the free-edge in, until there's a tiny gap and the remaining join results in almost parallel curves. The right hand image shows the result, which is significantly simpler than the $C_2$ case
5 $N$ surface		This shows what becomes of $N$ when it is stitched to $M$ along the $C_1$ and $C_2$ boundaries shown earlier, without $M$ drawn.
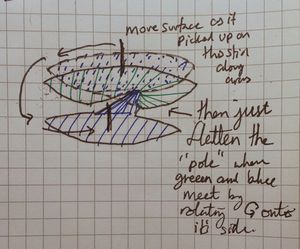
6 Final topological immersion		A diagram showing them together is very cluttered and hard to see (it either looks a mess, or a cylinder with a twist in the side), so I will show it like this. We see (a topological immersion) of $\mathbb{RP}^2$ in $\mathbb{R}^3$ is simply the union of a Möbius strip together with a "solid 8" shape, oo but joined. Take the left "disk" in this formation and lift it, then rotate it over the first disk in the formation. Showing $N$ is the joined oo I speak of. In this picture we imagine sticking a "stick" into the centre of the blue disk, on which the blue "wheel" can rotate freely, we move that stick along the arrows shown, the result is blue-and-green joined along a vertical pole. If you rotate that "pole" anticlockwise, so onto it's side, parallel to the x-axis on the paper it is drawn, you then have a $oo$ shape where the $o$ s are joined (that "pole" being the join between the two)