Exercises:Mond - Topology - 2/Section B/Question 6

Section B

Question 6

[ilmath]\xymatrix{ \bullet \ar@{<-}[dd]_B \ar@{<.}@/^1em/[rrr]^{(A)} \ar@{<-}[r]_{A_1} & \bullet \ar@{<-}[r]_{A_2} \ar@{}[ddr]|(.5){\mathbf{M} } \ar@{-->}@/_.65em/[dd]^{C_1} \ar@{-->}@/^.65em/[dd] & \bullet \ar@{<-}[r]_{A_3} \ar@{-->}@/_.65em/[dd]^{C_2} \ar@{-->}@/^.65em/[dd] & \bullet \\ & & &\\ \bullet \ar@{.>}@/_1em/[rrr]_{(A)} \ar[r]^{A_3} & \bullet \ar[r]^{A_2} & \bullet \ar[r]^{A_1} & \bullet \ar@{<-}[uu]_B }[/ilmath] 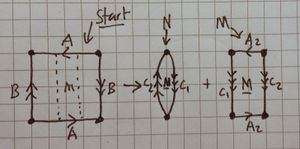We take [ilmath]\mathbb{RP}^2[/ilmath] (represented here as the gluings [ilmath]A[/ilmath] and [ilmath]B[/ilmath]) and cut it (creating gluings [ilmath]C_1[/ilmath] and [ilmath]C_2[/ilmath]), thus diving [ilmath]A[/ilmath] into [ilmath]A_1[/ilmath], [ilmath]A_2[/ilmath] and [ilmath]A_3[/ilmath]. The central strip is called [ilmath]M[/ilmath]

[ilmath]M[/ilmath] is a Mobius strip inside [ilmath]\mathbb{RP}^2[/ilmath]

The picture on the right shows that [ilmath]\mathbb{RP}^2[/ilmath] contains a Mobius strip, [ilmath]M[/ilmath]. Use the diagram, taking into account the glueings, to describe the complement of [ilmath]M[/ilmath] in [ilmath]\mathbb{RP}^2[/ilmath]. You mare allowed to cut it, provided you then glue it back together.

Complete the following sentence in as clear a way as possible:

• "[ilmath]\mathbb{RP}^2[/ilmath] is obtained from a Mobius strip by ....."

Solution

Step	Picture	Comment
1 Dividing up the square	We first take the square and cut it up, creating new edges for gluing, [ilmath]C_1[/ilmath] and [ilmath]C_2[/ilmath] (see the picture at the top of this question)	We do this then this To yield two "chunks", [ilmath]N[/ilmath] and [ilmath]M[/ilmath].
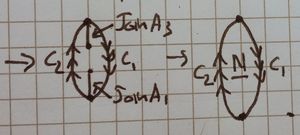
2 Making the Mobius band	We start with [ilmath]M[/ilmath] on the left.	Pretty self explanatory and routine, my pictures turned out really well, I am a little bit proud.
3 Joining the [ilmath]C_2[/ilmath] edges	v_2} part way around the [ilmath]C_2[/ilmath] edge of the band, then we let it return to [ilmath]v_1[/ilmath], [ilmath]v_1[/ilmath] and [ilmath]v_2[/ilmath] are added only for clarity. The next stage is purple, we stitch more of the edge along the [ilmath]C_2[/ilmath] edge of the band, then: Into blue, we pull it almost all the way round back to [ilmath]v_1[/ilmath]. Here the sum of the previous step is in green. We then pull the free edge inwards (red) until only a tiny amount of almost parallel [ilmath]C_2[/ilmath] join is left to do	this is the result The picture here shows only "half" of the [ilmath]N[/ilmath] surface, it is the result of stitching along the [ilmath]C_2[/ilmath] boundary.]]
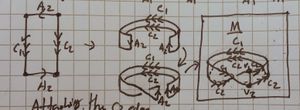
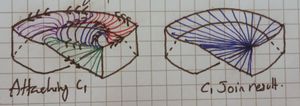
4 Joining the [ilmath]C_1[/ilmath] edge	We start with the green and just pull the [ilmath]C_1[/ilmath] edge along and start stitching. Then we pull that around - and stitch along the way - resulting in purple. Then we pull that almost all the way around yielding red. As before, we then pull the free-edge in, until there's a tiny gap and the remaining join results in almost parallel curves. The right hand image shows the result, which is significantly simpler than the [ilmath]C_2[/ilmath] case
5 [ilmath]N[/ilmath] surface