Basis and coordinates

This is very much a "motivation" page and a discussion of the topic.

See Change of basis matrix for the more maths aspect.

What is a coordinate

Suppose we have a Basis, a finite one, [math]\{b_1,...,b_n\}[/math], a point [ilmath]p[/ilmath] is given by [math]\sum^n_{k=1}a_ib_i[/math] and it is said to have coordinates [math](a_1,...,a_n)[/math] - because the basis set must be linearly independent, there is only one such [math](a_1,...,a_n)[/math] - hence "coordinate"

First example

Let us suppose we have two people working on squared paper, one of them is working on nice normal squared paper, the other one has found squared paper with squares half the length.

Immediately one sees that the point [ilmath](0,1)[/ilmath] in our space is [ilmath](0,2)[/ilmath] in theirs.

We will call their space "prime" space, so the coordinate [ilmath](x,y)[/ilmath] is on our paper, and [ilmath](x,y)'[/ilmath] or [ilmath](x',y')[/ilmath] is on their paper.

It is immediately obvious that [math](x,y)=(2x,2y)'[/math] but is this a linear transform? Well recall to be linear [math]T(ax+by)=aT(x)+bT(y)[/math]

Let us try it [math](ax_1+bx_2,ay_1+by_1)=(2ax_1+2bx_2,2ay_1+2by_2)'=a(2x_1,2y_1)'+b(2x_2,2y_2)'[/math]

This looks linear. So what is the change of basis matrix? Well without knowing that we can see quite obviously that:

[math]\begin{pmatrix}2 & 0 \\ 0 & 2\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}2x\\2y\end{pmatrix}[/math]

Formal definitions

• Let [math]S[/math] be our squared paper
• Let [math]S'[/math] be their squared paper
• Let [math]L:S\rightarrow S'[/math] be the transform that maps points on our paper to their paper.

Then the matrix form of L, denoted [math][L]_S^{S'}=\begin{pmatrix}2&0\\0&2\end{pmatrix}[/math]

Notice the notation [math][L]^\text{to}_\text{from}[/math]

Inverse

It is clear from simple thought that to go from [ilmath]S'[/ilmath] to [ilmath]S[/ilmath] the transform is simply [math](x,y)'=(\frac{1}{2}x,\frac{1}{2}y)[/math] and it is easy to show that this is linear. Let us call this map [ilmath]K[/ilmath] and define it as follows:

[math]K:S'\rightarrow S[/math] - then [math][K]_{S'}^S=\begin{pmatrix}\frac{1}{2}&0\\0&\frac{1}{2}\end{pmatrix}[/math]

This notation seems a little heavy and redundant (for example what would [math][K]_A^B[/math] mean? We will come to that later)

Combining things together

We now have the functions:

• [math]L:S\rightarrow S'[/math]
• [math]K:S'\rightarrow S[/math]

These are linear isomorpisms (they're bijective and linear) and just like functions we can compose them.

[math][L]_S^{S'}[K]_{S'}^S[/math] is the transform that takes a point in [ilmath]S[/ilmath] to [ilmath]S'[/ilmath] followed by another transform that takes that point in [ilmath]S'[/ilmath] to a point in [ilmath]S[/ilmath]

If you multiply these matrices (which I simply cannot be bothered to write) you will get the identity matrix, that is [math]([L]_S^{S'}[K]_{S'}^S)(x,y)=(x,y)[/math]

Introducing a third person

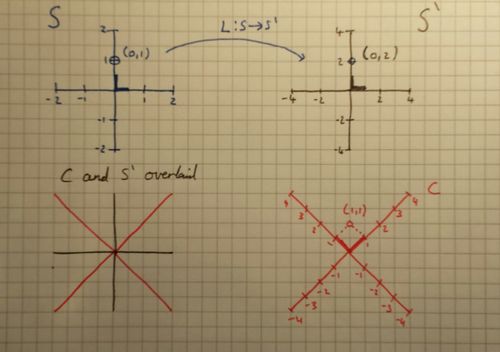
What we have so far, including third person. There is an error within the [ilmath]S[/ilmath] space, the blue thick lines representing basis vectors should be double their depicted length

The bold lines are the "basis" vectors, notice the unit square differs in all of these.

Rather than working out the transform from [ilmath]C[/ilmath] to [ilmath]S'[/ilmath] or whatever we can simply notice:

[math]\begin{pmatrix}a&\times \\ b&\times\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}[/math]

Recall the definition of coordinate, [math]\begin{pmatrix}1\\0\end{pmatrix}[/math] is the point [math]b_1[/math] (where [ilmath]b_1[/ilmath] is the first basis vector)

So this transform takes the first basis vector in one space to [math]\begin{pmatrix}a\\b\end{pmatrix}[/math] in another.

We will use [math](x,y)''[/math]to denote a point in [ilmath]C[/ilmath]

Coordinates again

It is clear from the diagram that [math](0,1)=(0,2)'=(1,1)''[/math]

=Computing the change of basis

So using [math]\begin{pmatrix}a&\times \\ b&\times\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}[/math] we wish to find a map

• [math][G]_S^C[/math]
• [math]G:S\rightarrow C[/math]

Either of these will do.

It is clear that [math](0,1)\mapsto(1,1)[/math] and [math](1,0)\mapsto(1,-1)[/math]