Difference between revisions of "Exercises:Mond - Topology - 1/Question 9"
(Finishing proof) |
m (Changes to picture caption) |
||
| Line 8: | Line 8: | ||
* We denote by {{M|\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} }} the [[canonical projection of the equivalence relation]], {{M|\sim}}. Note that this is a {{link|quotient map|topology}} when we consider {{M|\frac{\mathbb{S}^2}{\sim} }} with the [[quotient topology]]. | * We denote by {{M|\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} }} the [[canonical projection of the equivalence relation]], {{M|\sim}}. Note that this is a {{link|quotient map|topology}} when we consider {{M|\frac{\mathbb{S}^2}{\sim} }} with the [[quotient topology]]. | ||
====Solution outline==== | ====Solution outline==== | ||
| − | [[File:RP2isHausdorff.JPG|thumb| | + | [[File:RP2isHausdorff.JPG|thumb|Suppose we take the points {{M|\alpha}} and {{M|\beta}} on the sphere. We could have [[open ball|balls]] (in {{M|\mathbb{R}^3}}) that are centred at {{M|\alpha}} and {{M|\beta}} and they'd get quite large before touching (we want them to be disjoint!) However we must consider 4 open balls, one at each point {{M|\alpha}}, {{M|\beta}}, {{M|\gamma}} and {{M|\delta}}, we see here even though {{M|\alpha}} and {{M|\beta}} are far apart that {{M|\beta}} and {{M|\gamma}} (which is [[antipodal]] to {{M|\alpha}}) are actually rather close! |
| + | <br/><br/> | ||
| + | So rather than {{M|\epsilon\le\frac{1}{2}d(\alpha,\beta)}} (for {{M|d}} being the [[Euclidean metric]] of {{M|\mathbb{R}^3}}) we must make sure that the ball at the antipodal point doesn't touch any others too! | ||
| + | <br/><br/> | ||
| + | It is clear that if {{M|1=\epsilon\le\frac{1}{2} d(\alpha,\gamma)=1 }} that the balls centred at {{M|\alpha}} and {{M|\gamma}} (or {{M|\beta}} and {{M|\delta}}) wont touch, we must make sure that {{M|\alpha}} and {{M|\beta}} don't touch, so use {{M|\epsilon\le d(\alpha,\beta)}}. | ||
| + | <br/><br/> | ||
| + | But as the diagram shows, {{M|\alpha}} and {{M|\delta}} could be rather close! (or equivalently, {{M|\gamma}} and {{M|\beta}}), so we need {{M|\epsilon<\frac{1}{2} d(\alpha,\delta)}} too! | ||
| + | <br/><br/> | ||
| + | We can boil all these down into {{M|\epsilon\le\frac{1}{2}\text{min}(\{d(\alpha,\beta),d(\alpha,\delta)\})}} ]]<!-- | ||
| + | |||
| + | START OF PARAGRAPH AND END OF IMAGE HERE | ||
| + | |||
| + | -->We will deal with the [[open sets]], {{M|U}}, in terms of {{M|\pi^{-1}(U)}} (as by definition, {{M|U\in\mathcal{P}(\frac{\mathbb{S}^2}{\sim})}} is open in {{M|1=\frac{\mathbb{S}^2}{\sim} }} {{iff}} {{M|\pi^{-1}(U)}} is open in {{M|\mathbb{S}^2}}, which we consider with the [[subspace topology]] inherited from {{M|\mathbb{R}^3}} as usual) then we just have to find small enough open balls! | ||
With this in mind, let {{M|a,b\in\mathbb{RP}^2}} be given. We need to find two [[open sets]] (well... [[neighbourhoods]] will do... but open sets are neighbourhoods!), let's say {{M|U_a}} and {{M|U_b}} such that: | With this in mind, let {{M|a,b\in\mathbb{RP}^2}} be given. We need to find two [[open sets]] (well... [[neighbourhoods]] will do... but open sets are neighbourhoods!), let's say {{M|U_a}} and {{M|U_b}} such that: | ||
Revision as of 17:51, 11 October 2016
Contents
Section B
Question 9
The real projective plane, [ilmath]\mathbb{RP}^2[/ilmath] is defined as the quotient of the sphere, [ilmath]\mathbb{S}^2[/ilmath], by the equivalence relation that defines (for [ilmath]x\in\mathbb{S}^2\subset\mathbb{R}^3[/ilmath]) [ilmath]x\sim -x[/ilmath], that is it identifies antipodal points.
Show that [ilmath]\mathbb{RP}^2[/ilmath] is Hausdorff
Definitions
- We denote by [ilmath]\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} [/ilmath] the canonical projection of the equivalence relation, [ilmath]\sim[/ilmath]. Note that this is a quotient map when we consider [ilmath]\frac{\mathbb{S}^2}{\sim} [/ilmath] with the quotient topology.
Solution outline
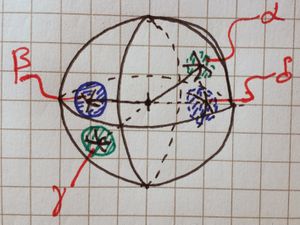
So rather than [ilmath]\epsilon\le\frac{1}{2}d(\alpha,\beta)[/ilmath] (for [ilmath]d[/ilmath] being the Euclidean metric of [ilmath]\mathbb{R}^3[/ilmath]) we must make sure that the ball at the antipodal point doesn't touch any others too!
It is clear that if [ilmath]\epsilon\le\frac{1}{2} d(\alpha,\gamma)=1[/ilmath] that the balls centred at [ilmath]\alpha[/ilmath] and [ilmath]\gamma[/ilmath] (or [ilmath]\beta[/ilmath] and [ilmath]\delta[/ilmath]) wont touch, we must make sure that [ilmath]\alpha[/ilmath] and [ilmath]\beta[/ilmath] don't touch, so use [ilmath]\epsilon\le d(\alpha,\beta)[/ilmath].
But as the diagram shows, [ilmath]\alpha[/ilmath] and [ilmath]\delta[/ilmath] could be rather close! (or equivalently, [ilmath]\gamma[/ilmath] and [ilmath]\beta[/ilmath]), so we need [ilmath]\epsilon<\frac{1}{2} d(\alpha,\delta)[/ilmath] too!
We can boil all these down into [ilmath]\epsilon\le\frac{1}{2}\text{min}(\{d(\alpha,\beta),d(\alpha,\delta)\})[/ilmath]
With this in mind, let [ilmath]a,b\in\mathbb{RP}^2[/ilmath] be given. We need to find two open sets (well... neighbourhoods will do... but open sets are neighbourhoods!), let's say [ilmath]U_a[/ilmath] and [ilmath]U_b[/ilmath] such that:
- [ilmath]a\in U_a[/ilmath], [ilmath]b\in U_b[/ilmath] and [ilmath]U_a\cap U_b=\emptyset[/ilmath]
Well:
- [ilmath]U_a[/ilmath] is open in [ilmath]\mathbb{RP}^2[/ilmath]
- [ilmath]\pi^{-1}(U_a)[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath]
- there exists an open set, [ilmath]V_a[/ilmath] in [ilmath]\mathbb{R}^3[/ilmath] such that [ilmath]V_a\cap\mathbb{S}^2=\pi^{-1}(U_a)[/ilmath]
Of course, the open balls of [ilmath]\mathbb{R}^3[/ilmath] are a basis, so we can think of [ilmath]V_a[/ilmath] as a union of open balls, or possibly just an open ball (as basis sets themselves are open, and also as an open ball can be expressed as a union of open balls).
This changes the question into, in terms of [ilmath]a[/ilmath] and [ilmath]b[/ilmath], what size balls can we consider in [ilmath]\mathbb{R}^3[/ilmath] such that they're disjoint. There's a caveat here. This is what is shown in the diagram.
If [ilmath]a[/ilmath] and [ilmath]b[/ilmath] are "far apart" on [ilmath]\mathbb{RP}^2[/ilmath], it is entirely possible (in the pre-image under [ilmath]\pi[/ilmath]) that the antipodal point of one is near the other!
So we must be careful to make sure our balls do not overlap at all!
Consider now [ilmath]\{x,-x\}=\pi^{-1}(a)[/ilmath] and [ilmath]\{y,-y\}=\pi^{-1}(b)[/ilmath]:
We notice also there is extra "structure" on [ilmath]\mathbb{R}^3[/ilmath], namely that it is a normed space, [ilmath](\mathbb{R}^3,\Vert\cdot\Vert)[/ilmath], and we consider the metric induced by the norm as the metric, [ilmath]d[/ilmath], for a metric space, [ilmath](\mathbb{R}^3,d)[/ilmath], then we see:
- [ilmath]d(x,y)=d(y,x)[/ilmath] (by the symmetric property of a metric) and
- [ilmath]d(-x,y)=\Vert -x-y\Vert = \Vert(-1)x+y\Vert=\Vert x+y\Vert=d(x,-y)[/ilmath]
- We don't need to consider [ilmath]d(x,-x)[/ilmath] and [ilmath]d(y,-y)[/ilmath], also [ilmath]d(x,x)=d(y,y)=0[/ilmath] is not very helpful
So take:
- [ilmath]\epsilon\le\frac{1}{2}\text{min}(\{d(x,y),d(x,-y)\})[/ilmath] (Note: Smaller would work too, eg [ilmath]\frac{1}{4} [/ilmath] rather than [ilmath]\frac{1}{2} [/ilmath] - I hope I don't need to prove [ilmath]\frac{1}{2} [/ilmath] is sufficient?)
- This should explain why [ilmath]d(x,-x)[/ilmath] and [ilmath]d(y,-y)[/ilmath] are of no use!
Then just place one of these open balls of radius [ilmath]\epsilon[/ilmath] at each of the 4 points. Job done!
Solution
We wish to show that [ilmath]\mathbb{RP}^2[/ilmath] is Hausdorff.
- Let [ilmath]a,b\in\mathbb{RP}^2[/ilmath] be given such that [ilmath]a\ne b[/ilmath], then
- there exist [ilmath]x,y\in\mathbb{S}^2[/ilmath] such that [ilmath]\pi^{-1}(a)=\{x,-x\}[/ilmath] and [ilmath]\pi^{-1}(b)=\{y,-y\}[/ilmath]
- Let [ilmath]\epsilon:=\frac{1}{2}\text{min}(\{d(x,y),d(x,-y)\})[/ilmath] Note that [ilmath]d(x,-y)=d(-x,y)[/ilmath] - see above in the outline section
- Let [ilmath]V_a:=B_\epsilon(x)\cup B_\epsilon(-x)\subset\mathbb{R}^3[/ilmath] and [ilmath]V_b:=B_\epsilon(y)\cup B_\epsilon(-y)\subset\mathbb{R}^3[/ilmath]. These are open (in [ilmath]\mathbb{R}^3[/ilmath]) as open balls are open sets, and the union of open sets is open.
- Now define [ilmath]U_a:=V_a\cap\mathbb{S}^2[/ilmath] and [ilmath]U_b:=V_b\cap\mathbb{S}^2[/ilmath], these are open in [ilmath]\mathbb{S}^2[/ilmath] (considered with the subspace topology it inherits from [ilmath]\mathbb{R}^3[/ilmath] - as mentioned in the outline)
- Recall [ilmath]U\in\mathcal{P}(\mathbb{RP}^2)[/ilmath] is open if and only if [ilmath]\pi^{-1}(U)[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath]
- Thus:
- [ilmath]\pi(U_a)[/ilmath] is open if and only if [ilmath]\pi^{-1}(\pi(U_a))[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath] and
- [ilmath]\pi(U_b)[/ilmath] is open if and only if [ilmath]\pi^{-1}(\pi(U_b))[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath]
- It should be clear that [ilmath]\pi^{-1}(\pi(U_a))=U_a[/ilmath] and [ilmath]\pi^{-1}(\pi(U_b))=U_b[/ilmath] (by their very construction)
- Thus:
- [ilmath]\pi(U_a)[/ilmath] is open if and only if [ilmath]\pi^{-1}(\pi(U_a))=U_a[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath] and
- [ilmath]\pi(U_b)[/ilmath] is open if and only if [ilmath]\pi^{-1}(\pi(U_b))=U_b[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath]
- As both right-hand-sides are true, we see [ilmath]\pi(U_a)[/ilmath] and [ilmath]\pi(U_b)[/ilmath] are both open in [ilmath]\mathbb{RP}^2[/ilmath]
- We must now show [ilmath]U_a[/ilmath] and [ilmath]U_b[/ilmath] are disjoint.
- Suppose there exists a [ilmath]p\in \pi(U_a)\cap\pi(U_b)[/ilmath] (that is that they're not disjoint and [ilmath]x[/ilmath] is in both of them), then:
- clearly [ilmath]\exists q\in \pi^{-1}(\pi(U_a))\cap\pi^{-1}(\pi(U_b))[/ilmath] such that [ilmath]\pi(q)=p[/ilmath][Note 1]
- However [ilmath]\pi^{-1}(\pi(U_a))\cap\pi^{-1}(\pi(U_b))=U_a\cap U_b[/ilmath] and [ilmath]U_a\cap U_b=\emptyset[/ilmath] (by construction), so there does not exist such a [ilmath]q[/ilmath]!
- If there is nothing in the pre-image of [ilmath]\pi(U_a)\cap\pi(U_b)[/ilmath] that maps to [ilmath]p[/ilmath] then we cannot have [ilmath]p\in \pi(U_a)\cap\pi(U_b)[/ilmath] - a contradiction
- clearly [ilmath]\exists q\in \pi^{-1}(\pi(U_a))\cap\pi^{-1}(\pi(U_b))[/ilmath] such that [ilmath]\pi(q)=p[/ilmath][Note 1]
- So there does not exist such a [ilmath]p[/ilmath], which means [ilmath]\pi(U_a)\cap\pi(U_b)=\emptyset[/ilmath], they're disjoint.
- Suppose there exists a [ilmath]p\in \pi(U_a)\cap\pi(U_b)[/ilmath] (that is that they're not disjoint and [ilmath]x[/ilmath] is in both of them), then:
- Now define [ilmath]U_a:=V_a\cap\mathbb{S}^2[/ilmath] and [ilmath]U_b:=V_b\cap\mathbb{S}^2[/ilmath], these are open in [ilmath]\mathbb{S}^2[/ilmath] (considered with the subspace topology it inherits from [ilmath]\mathbb{R}^3[/ilmath] - as mentioned in the outline)
- Let [ilmath]V_a:=B_\epsilon(x)\cup B_\epsilon(-x)\subset\mathbb{R}^3[/ilmath] and [ilmath]V_b:=B_\epsilon(y)\cup B_\epsilon(-y)\subset\mathbb{R}^3[/ilmath]. These are open (in [ilmath]\mathbb{R}^3[/ilmath]) as open balls are open sets, and the union of open sets is open.
- Let [ilmath]\epsilon:=\frac{1}{2}\text{min}(\{d(x,y),d(x,-y)\})[/ilmath] Note that [ilmath]d(x,-y)=d(-x,y)[/ilmath] - see above in the outline section
- there exist [ilmath]x,y\in\mathbb{S}^2[/ilmath] such that [ilmath]\pi^{-1}(a)=\{x,-x\}[/ilmath] and [ilmath]\pi^{-1}(b)=\{y,-y\}[/ilmath]
This completes the proof.
Notes
- ↑ Note that by Properties of the pre-image of a map that [ilmath]\pi^{-1}\big(\pi(U_a)\cap\pi(U_b)\big)=\pi^{-1}(\pi(U_a))\cap\pi^{-1}(\pi(U_b))[/ilmath]
References