Difference between revisions of "Exercises:Mond - Topology - 1/Question 9"
(Saving work) |
m (Altered formatting) |
||
| Line 5: | Line 5: | ||
Show that {{M|\mathbb{RP}^2}} is [[Hausdorff]] | Show that {{M|\mathbb{RP}^2}} is [[Hausdorff]] | ||
| − | ===Definitions=== | + | ====Definitions==== |
* We denote by {{M|\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} }} the [[canonical projection of the equivalence relation]], {{M|\sim}}. Note that this is a {{link|quotient map|topology}} when we consider {{M|\frac{\mathbb{S}^2}{\sim} }} with the [[quotient topology]]. | * We denote by {{M|\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} }} the [[canonical projection of the equivalence relation]], {{M|\sim}}. Note that this is a {{link|quotient map|topology}} when we consider {{M|\frac{\mathbb{S}^2}{\sim} }} with the [[quotient topology]]. | ||
| − | ===Solution outline=== | + | ====Solution outline==== |
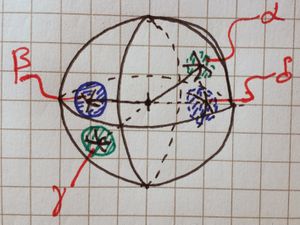
[[File:RP2isHausdorff.JPG|thumb|Diagram...]]We will deal with the [[open sets]], {{M|U}}, in terms of {{M|\pi^{-1}(U)}} (as by definition, {{M|U\in\mathcal{P}(\frac{\mathbb{S}^2}{\sim})}} is open in {{M|1=\frac{\mathbb{S}^2}{\sim} }} {{iff}} {{M|\pi^{-1}(U)}} is open in {{M|\mathbb{S}^2}}, which we consider with the [[subspace topology]] inherited from {{M|\mathbb{R}^3}} as usual) then we just have to find small enough open balls! | [[File:RP2isHausdorff.JPG|thumb|Diagram...]]We will deal with the [[open sets]], {{M|U}}, in terms of {{M|\pi^{-1}(U)}} (as by definition, {{M|U\in\mathcal{P}(\frac{\mathbb{S}^2}{\sim})}} is open in {{M|1=\frac{\mathbb{S}^2}{\sim} }} {{iff}} {{M|\pi^{-1}(U)}} is open in {{M|\mathbb{S}^2}}, which we consider with the [[subspace topology]] inherited from {{M|\mathbb{R}^3}} as usual) then we just have to find small enough open balls! | ||
| Line 25: | Line 25: | ||
So we must be careful to make sure our balls do not overlap at all! | So we must be careful to make sure our balls do not overlap at all! | ||
| − | ===Solution=== | + | ====Solution==== |
We wish to show that {{M|\mathbb{RP}^2}} is [[Hausdorff]]. | We wish to show that {{M|\mathbb{RP}^2}} is [[Hausdorff]]. | ||
* Let {{M|a,b\in\mathbb{RP}^2}} be given such that {{M|1=a\ne b}}, then | * Let {{M|a,b\in\mathbb{RP}^2}} be given such that {{M|1=a\ne b}}, then | ||
Revision as of 18:34, 10 October 2016
Contents
Section B
Question 9
The real projective plane, [ilmath]\mathbb{RP}^2[/ilmath] is defined as the quotient of the sphere, [ilmath]\mathbb{S}^2[/ilmath], by the equivalence relation that defines (for [ilmath]x\in\mathbb{S}^2\subset\mathbb{R}^3[/ilmath]) [ilmath]x\sim -x[/ilmath], that is it identifies antipodal points.
Show that [ilmath]\mathbb{RP}^2[/ilmath] is Hausdorff
Definitions
- We denote by [ilmath]\pi:\mathbb{S}^2\rightarrow\frac{\mathbb{S}^2}{\sim} [/ilmath] the canonical projection of the equivalence relation, [ilmath]\sim[/ilmath]. Note that this is a quotient map when we consider [ilmath]\frac{\mathbb{S}^2}{\sim} [/ilmath] with the quotient topology.
Solution outline
We will deal with the open sets, [ilmath]U[/ilmath], in terms of [ilmath]\pi^{-1}(U)[/ilmath] (as by definition, [ilmath]U\in\mathcal{P}(\frac{\mathbb{S}^2}{\sim})[/ilmath] is open in [ilmath]\frac{\mathbb{S}^2}{\sim}[/ilmath] if and only if [ilmath]\pi^{-1}(U)[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath], which we consider with the subspace topology inherited from [ilmath]\mathbb{R}^3[/ilmath] as usual) then we just have to find small enough open balls!With this in mind, let [ilmath]a,b\in\mathbb{RP}^2[/ilmath] be given. We need to find two open sets (well... neighbourhoods will do... but open sets are neighbourhoods!), let's say [ilmath]U_a[/ilmath] and [ilmath]U_b[/ilmath] such that:
- [ilmath]a\in U_a[/ilmath], [ilmath]b\in U_b[/ilmath] and [ilmath]U_a\cap U_b=\emptyset[/ilmath]
Well:
- [ilmath]U_a[/ilmath] is open in [ilmath]\mathbb{RP}^2[/ilmath]
- [ilmath]\pi^{-1}(U_a)[/ilmath] is open in [ilmath]\mathbb{S}^2[/ilmath]
- there exists an open set, [ilmath]V_a[/ilmath] in [ilmath]\mathbb{R}^3[/ilmath] such that [ilmath]V_a\cap\mathbb{S}^2=\pi^{-1}(U_a)[/ilmath]
Of course, the open balls of [ilmath]\mathbb{R}^3[/ilmath] are a basis, so we can think of [ilmath]V_a[/ilmath] as a union of open balls, or possibly just an open ball (as basis sets themselves are open, and also as an open ball can be expressed as a union of open balls).
This changes the question into, in terms of [ilmath]a[/ilmath] and [ilmath]b[/ilmath], what size balls can we consider in [ilmath]\mathbb{R}^3[/ilmath] such that they're disjoint. There's a caveat here. This is what is shown in the diagram.
If [ilmath]a[/ilmath] and [ilmath]b[/ilmath] are "far apart" on [ilmath]\mathbb{RP}^2[/ilmath], it is entirely possible (in the pre-image under [ilmath]\pi[/ilmath]) that the antipodal point of one is near the other!
So we must be careful to make sure our balls do not overlap at all!
Solution
We wish to show that [ilmath]\mathbb{RP}^2[/ilmath] is Hausdorff.
- Let [ilmath]a,b\in\mathbb{RP}^2[/ilmath] be given such that [ilmath]a\ne b[/ilmath], then
- there exist [ilmath]x,y\in\mathbb{S}^2[/ilmath] such that [ilmath]\pi^{-1}(a)=\{x,-x\}[/ilmath] and [ilmath]\pi^{-1}(b)=\{y,-y\}[/ilmath]
Notes
References