Difference between revisions of "Exercises:Mond - Topology - 1/Question 6"

Revision as of 12:54, 8 October 2016

Section A

Question 6

Part I

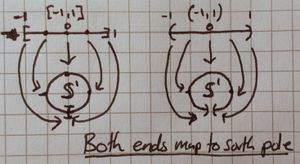
Find a surjective continuous mapping from [ilmath][-1,1]\subset\mathbb{R} [/ilmath] to the unit circle, [ilmath]\mathbb{S}^1[/ilmath] such that it is injective except for that it sends [ilmath]-1[/ilmath] and [ilmath]1[/ilmath] to the same point in [ilmath]\mathbb{S}^1[/ilmath]. Definitions may be explicit or use a picture

Solution

Take -1 to any point on the circle (we pick the south pole in this diagram), then go around the circle clockwise at a constant speed such that by [ilmath]f(1)[/ilmath] one has done a full revolution and is back at the starting point.

The right-hand-side is intended to demonstrate that the interval [ilmath](-1,1)[/ilmath] to the circle without the south-pole is bijective, ie it is injective and surjective, so the diagram on the left is "almost injective" in that it is injective everywhere except that it maps [ilmath]-1[/ilmath] and [ilmath]1[/ilmath] both to the south pole.
As required

• [ilmath]f:t\mapsto\begin{pmatrix}\cos(\pi(t+1))\\\sin(\pi(t+1))\end{pmatrix} [/ilmath], this starts at the point [ilmath](1,0)[/ilmath] and goes anticlockwise around the circle of unit radius once.
  • Note: I am not asked to show this is continuous, merely exhibit it.

Part 2

Define an equivalence relation on [ilmath][-1,1][/ilmath] by declaring [ilmath]-1\sim 1[/ilmath], use part 1 above and applying the topological version of passing to the quotient to find a continuous bijection: [ilmath](:[-1,1]/\sim\rightarrow\mathbb{S}^1)[/ilmath]

Solution

We wish to apply passing to the quotient. Notice:

1. we get [ilmath]\pi:[-1,1]\rightarrow[-1,1]/\sim[/ilmath], [ilmath]\pi:x\mapsto [x][/ilmath] automatically and it is continuous.
2. we've already got a map, [ilmath]f[/ilmath], of the form [ilmath](:[-1,1]\rightarrow\mathbb{S}^1)[/ilmath]

In order to use the theorem we must show:

• "[ilmath]f[/ilmath] is constant on the fibres of [ilmath]\pi[/ilmath]", that is:
  • [ilmath]\forall x,y\in [-1,1][\pi(x)=\pi(y)\implies f(x)=f(y)][/ilmath]
• Proof:
  • Let [ilmath]x,y\in[-1,1][/ilmath] be given
    • Suppose [ilmath]\pi(x)\ne\pi(y)[/ilmath], by the nature of implies we do not care about the RHS of the implication, true or false, the implication holds, so we're done
    • Suppose [ilmath]\pi(x)=\pi(y)[/ilmath], we must show that this means [ilmath]f(x)=f(y)[/ilmath]
      • It is easy to see that if [ilmath]x\in(-1,1)\subset\mathbb{R} [/ilmath] then [ilmath]\pi(x)=\pi(y)\implies y=x[/ilmath]
        • By the nature of [ilmath]f[/ilmath] being a function (only associating an element of the domain with one thing in the codomain) and having [ilmath]y=x[/ilmath] we must have: [ilmath]f(x)=f(y)[/ilmath]
      • Suppose [ilmath]x\in\{-1,1\} [/ilmath], it is easy to see that then [ilmath]\pi(x)=\pi(y)\implies y\in\{-1,1\}[/ilmath]
        • But [ilmath]f(-1)=f(1)[/ilmath] so, whichever the case, [ilmath]f(x)=f(y)[/ilmath]

We may now apply the theorem to yield:

• a unique continuous map, [ilmath]\overline{f}:[-1,1]/\sim\rightarrow\mathbb{S}^1[/ilmath] such that [ilmath]f=\overline{f}\circ\pi[/ilmath]

The question requires us to show this is a bijection, we must show that [ilmath]\newcommand{\fbar}{\bar{f} }\fbar[/ilmath] is both injective and surjective:

1. Surjective: [ilmath]\forall y\in \mathbb{S}^1\exists x\in [-1,1]/\sim[\fbar(x)=y][/ilmath] Caution:I should really factor this out into its own proposition
   • Let [ilmath]y\in \mathbb{S}^1[/ilmath] be given.
     • Note that [ilmath]f[/ilmath] is surjective, and [ilmath]f=\fbar\circ\pi[/ilmath], thus [ilmath]\exists p\in[-1,1][/ilmath] such that [ilmath]p=f^{-1}(y)=(\fbar\circ\pi)^{-1}(y)=\pi^{-1}(\fbar^{-1}(y))[/ilmath], thus [ilmath]\pi(p)=\fbar^{-1}(y)[/ilmath]
     • Choose [ilmath]x\in[-1,1]/\sim[/ilmath] to be [ilmath]\pi(p)[/ilmath] where [ilmath]p\in[-1,1][/ilmath] exists by surjectivity of [ilmath]f[/ilmath] and is such that [ilmath]f(p)=y[/ilmath]
       • Now [ilmath]\fbar(\pi(p))=f(p)[/ilmath] (by definition of [ilmath]\fbar[/ilmath]) and [ilmath]f(p)=y[/ilmath], as required.
2. Injective:
   • Caution:Do later on paper, it is easy to see though as [ilmath]f\big\vert_{(-1,1)} [/ilmath] is clearly injective, that covers all of [ilmath]\mathbb{S}^1[/ilmath] except [ilmath]f(1)=f(-1)[/ilmath], it is clear that if [ilmath]\fbar(x)=f(1)[/ilmath] that [ilmath]x[/ilmath] can only be [ilmath]\pi(-1)=\pi(1)[/ilmath]

Thus [ilmath]\fbar[/ilmath] is a bijection

Part 3

Show that [ilmath][-1,1]/\sim[/ilmath] is homeomorphic to [ilmath]\mathbb{S}^1[/ilmath]

Solution

To apply the "compact-to-Hausdorff theorem" we require:

1. A continuous bijection, which we have, namely [ilmath]\fbar:\frac{[-1,1]}{\sim}\rightarrow\mathbb{S}^1[/ilmath]
2. the domain space, [ilmath]\frac{[-1,1]}{\sim} [/ilmath], to be compact, and
3. the codomain space, [ilmath]\mathbb{S}^1[/ilmath], to be Hausdorff

We know the image of a compact set is compact, and that closed intervals are compact in [ilmath]\mathbb{R} [/ilmath], thus [ilmath][-1,1]/\sim=\pi([1-,1])[/ilmath] must be compact. We also know [ilmath]\mathbb{R}^2[/ilmath] is Hausdorff and every subspace of a Hausdorff space is Hausdorff, thus [ilmath]\mathbb{S}^1[/ilmath] is Hausdorff.

We apply the theorem:

• [ilmath]\fbar[/ilmath] is a homeomorphism

Notes

References