Difference between revisions of "Exercises:Mond - Topology - 1"

Revision as of 11:31, 8 October 2016

Section A

Section B

Exercises 6, 7 and 8 make use of the compact-to-Hausdorff theorem

Question 6

Part I

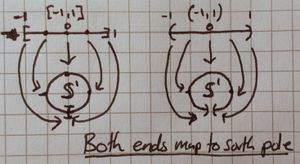
Find a surjective continuous mapping from $[-1,1]\subset\mathbb{R}$ to the unit circle, $\mathbb{S}^1$ such that it is injective except for that it sends $-1$ and $1$ to the same point in $\mathbb{S}^1$. Definitions may be explicit or use a picture

Solution

Take -1 to any point on the circle (we pick the south pole in this diagram), then go around the circle clockwise at a constant speed such that by $f(1)$ one has done a full revolution and is back at the starting point.

The right-hand-side is intended to demonstrate that the interval $(-1,1)$ to the circle without the south-pole is bijective, ie it is injective and surjective, so the diagram on the left is "almost injective" in that it is injective everywhere except that it maps $-1$ and $1$ both to the south pole.
As required

• $f:t\mapsto\begin{pmatrix}-\sin(\pi(t+1))\\-\cos(\pi(t+1))\end{pmatrix}$, this starts at the point $(1,0)$ and goes anticlockwise around the circle of unit radius once.
  • Note: I am not asked to show this is continuous, merely exhibit it.
  • Note: The reason for the odd choice of $\sin$ for the $x$ coordinate, and the minus signs is because my first choice was $f:t\mapsto\begin{pmatrix}\cos(\pi(t+1))\\\sin(\pi(t+1))\end{pmatrix}$, however that didn't match up with the picture. The picture goes clockwise from the south pole, this would go anticlockwise from the east pole.

Part 2

Define an equivalence relation on $[-1,1]$ by declaring $-1\sim 1$, use part 1 above and applying the topological version of passing to the quotient to find a continuous bijection: $(:\frac{[-1,1]}{\sim}\rightarrow\mathbb{S}^1)$

Solution

We wish to apply passing to the quotient. Notice:

1. we get $\pi:[-1,1]\rightarrow\frac{[-1,1]}{\sim}$, $\pi:x\mapsto [x]$ automatically and it is continuous.
2. we've already got a map, $f$, of the form $(:[-1,1]\rightarrow\mathbb{S}^1)$

In order to use the theorem we must show:

• "$f$ is constant on the fibres of $\pi$", that is:
  • $\forall x,y\in [-1,1][\pi(x)=\pi(y)\implies f(x)=f(y)]$
• Proof:
  • Let $x,y\in[-1,1]$ be given
    • Suppose $\pi(x)\ne\pi(y)$, by the nature of implies we do not care about the RHS of the implication, true or false, the implication holds, so we're done
    • Suppose $\pi(x)=\pi(y)$, we must show that this means $f(x)=f(y)$
      • It is easy to see that if $x\in(-1,1)\subset\mathbb{R}$ then $\pi(x)=\pi(y)\implies y=x$
        • By the nature of $f$ being a function (only associating an element of the domain with one thing in the codomain) and having $y=x$ we must have: $f(x)=f(y)$
      • Suppose $x\in\{-1,1\}$, it is easy to see that then $\pi(x)=\pi(y)\implies y\in\{-1,1\}$
        • But $f(-1)=f(1)$ so, whichever the case, $f(x)=f(y)$

We may now apply the theorem to yield:

• a unique continuous map, $\overline{f}:[-1,1]/\sim\rightarrow\mathbb{S}^1$ such that $f=\overline{f}\circ\pi$

The question requires us to show this is a bijection, we must show that $\newcommand{\fbar}{\bar{f} }\fbar$ is both injective and surjective:

1. Surjective: $\forall y\in \mathbb{S}^1\exists x\in \frac{[-1,1]}{\sim}[\fbar(x)=y]$
   • There are two ways to do this:
     1. Note that (from passing to the quotient) that if $f$ is surjective, then the resulting $\fbar$ is surjective.
     2. Or the long way of showing the definition of $\fbar$ being a surjection, $\forall y\in\mathbb{S}^1\exists x\in\frac{[-1,1]}{\sim}[\fbar(x)=y]$
        • Let $y\in \mathbb{S}^1$ be given.
          • Note that $f$ is surjective, and $f=\fbar\circ\pi$, thus $\exists p\in[-1,1]$ such that $p=f^{-1}(y)=(\fbar\circ\pi)^{-1}(y)=\pi^{-1}(\fbar^{-1}(y))$, thus $\pi(p)=\fbar^{-1}(y)$
          • Choose $x\in[-1,1]/\sim$ to be $\pi(p)$ where $p\in[-1,1]$ exists by surjectivity of $f$ and is such that $f(p)=y$
            • Now $\fbar(\pi(p))=f(p)$ (by definition of $\fbar$) and $f(p)=y$, as required.
2. Injective:
   • Let $x,y\in\frac{[-1,1]}{\sim}$ be given. We wish to show that $\fbar(x)=\fbar(y)\implies x=y$
     • Suppose $\fbar(x)\ne\fbar(y)$, then we're done, as by the nature of logical implication we do not care about the right hand side.
       • Note though, by the definition of $\fbar$ being a function we cannot have $x=y$ in this case! As a function must map each element of the domain to exactly one thing of the codomain. Anyway!
     • Suppose $\fbar(x)=\fbar(y)$, we must show that in this case we have $x=y$.
       • By surjectivity of $\pi:[-1,1]\rightarrow\frac{[-1,1]}{\sim}$ we see $\exists a\in [-1,1]\big[\pi(a)=x\big]$ and $\exists b\in [-1,1]\big[\pi(b)=y\big]$
         • Notice now we have $\fbar(x)=\fbar(\pi(a))$ and that (from the passing to the quotient part of obtaining $\fbar$) we have $f=\fbar\circ\pi$, this means:
           • $\fbar(x)=\fbar(\pi(a))=f(a)$, we also have $\fbar(y)=\fbar(\pi(b))=f(b)$ from the same thoughts, but using $y$ and $b$ instead of $x$ and $a$.
         • In particular: $f(a)=f(b)$
         • Now we have two cases, $a\in(-1,1)$ and $a\in\{-1,1\}$, we shall deal with them separately.
           1. We have $f(a)=f(b)$, suppose $a\in(-1,1)$
              • Recall that our very definition of $f$ required it to be "almost injective", specifically that $f\big\vert_{(-1,1)}:(-1,1)\rightarrow\mathbb{S}^1$ was injective (and that it was only "not injective" on the endpoints)
              • As $f$ is "injective in this range" we see that to have $f(a)=f(b)$ means $a=b$ (by injectiveness of $f\big\vert_{(-1,1)}$)
                • As $a=b$ we see $y=\pi(b)=\pi(a)=x$ and conclude $y=x$ - as required.
           2. We have $f(a)=f(b)$, and this time $a\in\{-1,1\}$ instead
              • Again by definition of $f$, we recall $f(-1)=f(1)$ - it maps the endpoints of $[-1,1]$ to the same point in $\mathbb{S}^1$.
              • To have $f(a)=f(b)$ clearly means that $b\in\{-1,1\}$ (regardless of what value $a\in\{-1,1\}$ takes)
                • But $\pi(a)=[a]=\{-1,1\}$ and also $\pi(b)=[b]=\{-1,1\}$
                • So we see $y=\pi(b)=\{-1,1\}=\pi(a)=x$, explicitly: $x=y$, as required
         • We have shown that in either case $x=y$
   • Since $x,y\in\frac{[-1,1]}{\sim}$ was arbitrary, we have shown this for all $x,y$. The very definition of $\fbar$ being injective.

Thus $\fbar$ is a bijection

Part 3

Show that $[-1,1]/\sim$ is homeomorphic to $\mathbb{S}^1$

Solution

To apply the "compact-to-Hausdorff theorem" we require:

1. A continuous bijection, which we have, namely $\fbar:\frac{[-1,1]}{\sim}\rightarrow\mathbb{S}^1$
2. the domain space, $\frac{[-1,1]}{\sim}$, to be compact, and
3. the codomain space, $\mathbb{S}^1$, to be Hausdorff

We know the image of a compact set is compact, and that closed intervals are compact in $\mathbb{R}$, thus $[-1,1]/\sim=\pi([1-,1])$ must be compact. We also know $\mathbb{R}^2$ is Hausdorff and every subspace of a Hausdorff space is Hausdorff, thus $\mathbb{S}^1$ is Hausdorff.

We apply the theorem:

• $\fbar$ is a homeomorphism

Question 7

Let $D^2$ denote the closed unit disk in $\mathbb{R}^2$ and define an equivalence relation on $D^2$ by setting $x_1\sim x_2$ if $\Vert x_1\Vert=\Vert x_2\Vert=1$ ("collapsing the boundary to a single point"). Show that $\frac{D^2}{\sim}$ is homeomorphic to $\mathbb{S}^2$ - the sphere.

• Hint: first define a surjection $(:D^2\rightarrow\mathbb{S}^2)$ mapping all of $\partial D^2$ to the north pole. This may be defined using a good picture or a formula.

Solution

The idea is to double the radius of $D^2$, then pop it out into a hemisphere, then pull the rim to a point

Picture showing the "expanding $D^2$", the embedding-in-$\mathbb{R}^3$ part, and the "popping out"

Definitions:

• $H$ denotes the hemisphere in my picture.
• $E:D^2\rightarrow H$ is the composition of maps in my diagram that take $D^2$, double its radius, then embed it in $\mathbb{R}^3$ then "pop it out" into a hemisphere. We take it as obvious that it is a homeomorphism
• $f':H\rightarrow\mathbb{S}^2$, this is the map in the top picture. It takes the hemisphere and pulls the boundary/rim in (along the blue lines) to the north pole of the red sphere. $f'(\partial H)=(0,0,1)\in\mathbb{R}^3$, it should be clear that for all $x\in H-\partial H$ that $f'(x)$ is intended to be a point on the red sphere and that $f'\big\vert_{H-\partial H}$ is injective. It is also taken as clear that $f'$ is surjective
• Note: Click the pictures for a larger version
• $\frac{D^2}{\sim}$ and $D^2/\sim$ denote the quotient space, with this definition we get a canonical projection, $\pi:D^2\rightarrow D^2/\sim$ given by $\pi:x\mapsto [x]$ where $[x]$ denotes the equivalence class of $x$
• Lastly, we define $f:D^2\rightarrow\mathbb{S}^2$ to be the composition of $E$ and $f'$, that is: $f:=f'\circ E$, meaning $f:x\mapsto f'(E(x))$

The situation is shown diagramatically below:

• $\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f:=f'\circ E} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} }$

Outline of the solution:

• We then want apply the passing to the quotient theorem to yield a commutative diagram: $\xymatrix{ D^2 \ar[d]_\pi \ar[r]^E \ar@/^1.5pc/[rr]^{f} & H \ar[r]^{f'} & \mathbb{S}^2 \\ \frac{D^2}{\sim} \ar@{.>}[urr]_{\bar{f} } }$
  • The commutative diagram part merely means that $f=\bar{f}\circ\pi$^{[Note 1]}. We get $f=\bar{f}\circ\pi$ as a result of the passing-to-the-quotient theorem.
  • We take this diagram as showing morphisms in the TOP category, meaning all arrows shown represent continuous maps. (Obviously...)
• Lastly, we will show that $\bar{f}$ is a homeomorphism using the compact-to-Hausdorff theorem

Solution body

First we must show the requirements for applying passing to the quotient are satisfied.

• We know already the maps involved are continuous and that $\pi$ is a quotient map. We only need to show:
  • $f$ is constant on the fibres of $\pi$, which is equivalent to:
    • $\forall x,y\in D^2[\pi(x)=\pi(y)\implies f(x)=f(y)]$
• Let us show this remaining condition:
  • Let $x,y\in D^2$ be given.
    • Suppose $\pi(x)\ne\pi(y)$, then by the nature of logical implication the implication is true regardless of $f(x)$ and $f(y)$'s equality. We're done in this case.
    • Suppose $\pi(x)=\pi(y)$, we must show that in this case $f(x)=y(y)$.
      • Suppose $x\in D^2-\partial D^2$ (meaning $x\in D^2$ but $x\notin \partial D^2$, ie $-$ denotes relative complement)
        • In this case we must have $x=y$, as otherwise we'd not have $\pi(x)=\pi(y)$ (for $x\in D^2-\partial D^2$ we have $\pi(x)=[x]=\{x\}$, that is that the equivalence classes are singletons. So if $\pi(x)=\pi(y)$ we must have $\pi(y)=[y]=\{x\}=[x]=\pi(x)$; so $y$ can only be $x$)
        • If $x=y$ then by the nature of $f$ being a function we must have $f(x)=f(y)$, we're done in this case
      • Suppose $x\in \partial D^2$ (the only case not covered) and $\pi(x)=\pi(y)$, we must show $f(x)=f(y)$
        • Clearly if $x\in\partial D^2$ and $\pi(x)=\pi(y)$ we must have $y\in\partial D^2$.
          • $E(x)$ is mapped to the boundary/rim of $H$, as is $E(y)$ and $f'(\text{any point on the rim of }H)=(0,0,1)\in\mathbb{R}^3$
          • Thus $f'(E(x))=f'(E(y))$, but $f'(E(x))$ is the very definition of $f(x)$, so clearly:
            • $f(x)=f(y)$ as required.

We may now apply the passing to the quotient theorem. This yields:

• A continuous map, $\bar{f}:D^2/\sim\rightarrow\mathbb{S}^2$ where $f=\bar{f}\circ\pi$

In order to apply the compact-to-Hausdorff theorem and show $\bar{f}$ is a homeomorphism we must show it is continuous and bijective. We already have continuity (as a result of the passing-to-the-quotient theorem), we must show it is bijective.

We must show $\bar{f}$ is both surjective and injective:

1. Surjectivity: We can get this from the definition of $\bar{f}$, recall on the passing to the quotient (function) page that:
   • if $f$ is surjective then $\bar{f}$ (or $\tilde{f}$ as the induced function is on that page) is surjective also
     • I've already done it "the long way" once in this assignment, and I hope it is not frowned upon if I decline to do it again.
2. Injectivity: This follows a similar to gist as to what we've done already to show we could apply "passing to the quotient" and for the other questions where we've had to show a factored map is injective. As before:
   • Let $x,y\in\frac{D^2}{\sim}$ be given.
     • Suppose $\bar{f}(x)\ne\bar{f}(y)$ - then by the nature of logical implication we do not care about the RHS and are done regardless of $x$ and $y$'s equality
       • Once again I note we must really have $x\ne y$ as if $x=y$ then by definition of $\bar{f}$ being a function we must also have $\bar{f}(x)=\bar{f}(y)$, anyway!
     • Suppose that $\bar{f}(x)=\bar{f}(y)$, we must show that in this case $x=y$.
       • Note that by surjectivity of $\pi$ that: $\exists a\in D^2[\pi(a)=x]$ and $\exists b\in D^2[\pi(b)=y]$, so $\bar{f}(x)=\bar{f}(\pi(a))$ and $\bar{f}(y)=\bar{f}(\pi(b))$, also, as $\bar{f}$ was the result of factoring, we have $f=\bar{f}\circ\pi$, so we see $\bar{f}(\pi(a))=f(a)$ and $\bar{f}(\pi(b))=f(b)$, since $\bar{f}(x)=\bar{f}(y)$ we get $f(a)=f(b)$ and $\bar{f}(\pi(a))=\bar{f}(\pi(b))$ also.
         • We now have 2 cases, $a\in D^2-\partial D^2$ and $a\in \partial D^2$ respectively:
           1. Suppose $a\in D^2-\partial D^2$
              • As we have $f(a)=f(b)$ we must have $b=a$, as if $b\ne a$ then $f(b)\ne f(a)$, because $f\big\vert_{D^2-\partial D^2}:(D^2-\partial D^2)\rightarrow\mathbb{S}^2$ is injective^{[Note 2]} by construction
                • If $b=a$ then $y=\pi(b)=\pi(a)=x$ so $y=x$ as required (this is easily recognised as $x=y$)
           2. Suppose $a\in\partial D^2$
              • Then to have $f(a)=f(b)$ we must have $b\in\partial D^2$
                • This means $a\sim b$, and that means $\pi(a)=\pi(b)$
                  • But $y=\pi(b)$ and $x=\pi(a)$, so we arrive at: $x=\pi(a)=\pi(b)=y$, or $x=y$, as required.

We now know $\bar{f}$ is a continuous bijection.

Noting that $D^2$ is closed and bounded we can apply the Heine–Borel theorem to show $D^2$ is compact. As $\pi:D^2\rightarrow\frac{D^2}{\sim}$ is continuous (see quotient topology for information) we can use "the image of a compact set is compact" to conclude that $\frac{D^2}{\sim}$ is compact.

A subspace of a Hausdorff space is a Hausdorff space, as $\mathbb{S}^2$ is a topological subspace of $\mathbb{R}^3$, $\mathbb{S}^2$ is Hausdorff.

We may now use the compact-to-Hausdorff theorem (as $\bar{f}$ is a bijective continuous map between a compact space to a Hausdorff space) to show that $\bar{f}$ is a homeomorphism

As we have found a homeomorphism between $\frac{D^2}{\sim}$ and $\mathbb{S}^2$ we have shown they are homeomorphic, written:

• $\frac{D^2}{\sim}\cong\mathbb{S}^2$.

Section C

Notes

1. Jump up ↑ Technically a diagram is said to commute if all paths through it yield equal compositions, this means that we also require $f=f'\circ E$, which we already have by definition of $f$!
2. Jump up ↑ Actually:
   • $f\big\vert_{D^2-\partial D^2}:(D^2-\partial D^2)\rightarrow(\mathbb{S}^2-\{(0,0,1)\})$ is bijective in fact!

References