Difference between revisions of "Limit (sequence)"
From Maths
m (→Process) |
m (→Cauchy sequence) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 51: | Line 51: | ||
==Discussion== | ==Discussion== | ||
===Requiring {{M|x\in X}}=== | ===Requiring {{M|x\in X}}=== | ||
| − | If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}} | + | If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}}. |
| + | |||
| + | To sidestep this limitation and talk about sequences that would converge if only their limit was in the space we consider [[Cauchy sequence|Cauchy sequences]]. It is easy to see that all convergent sequences are Cauchy: | ||
| + | ====[[Cauchy sequence]]==== | ||
| + | Recall a [[Cauchy sequence]] is defined as:<br/> | ||
| + | {{:Cauchy sequence/Short definition}} | ||
| + | {{Begin Theorem}} | ||
| + | [[Every convergent sequence is Cauchy]] | ||
| + | {{Begin Proof}} | ||
| + | {{:Every convergent sequence is Cauchy/Proof}} | ||
| + | {{End Proof}}{{End Theorem}} | ||
| + | |||
===Process=== | ===Process=== | ||
{{Begin Theorem}} | {{Begin Theorem}} | ||
Latest revision as of 13:56, 5 December 2015
- Note: see Limit page for other kinds of limits
Contents
[<hidetoc>]Definition
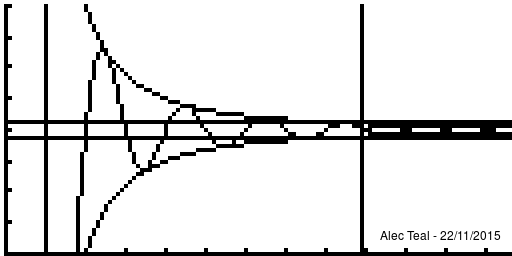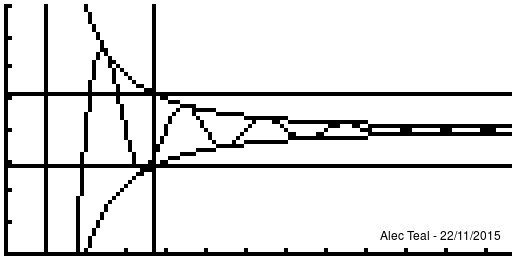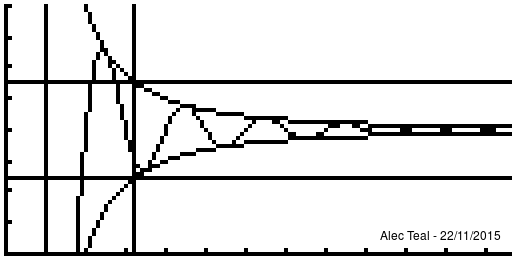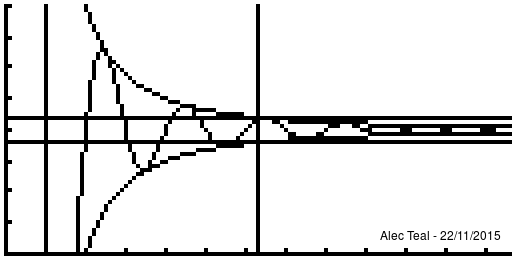
Given a sequence (xn)∞n=1⊆X, a metric space (X,d) (that is complete) and a point x∈X, the sequence (xn) is said to[1][Note 1]:
- have limit x or converge to x
When:
- ∀ϵ>0∃N∈N∀n∈N[n>N⟹d(x,xn)<ϵ][Note 2]
- (note that ϵ∈R, obviously - as the co-domain of d is R)
- Read this as:
- for all ϵ greater than zero, there exists an N in the natural numbers such that for all n that are also natural we have that:
- whenever n is beyond N that xn is within ϵ of x
- for all ϵ greater than zero, there exists an N in the natural numbers such that for all n that are also natural we have that:
Equivalent definitions
- Note: where it is not obvious changes have a { underneath them
[<collapsible-expand>]
lim
Discussion
Requiring x\in X
If x\notin X then d(x_n,x) is undefined, as d:X\times X\rightarrow\mathbb{R}_{\ge_0} , that is the distance metric is only defined for things in X.
To sidestep this limitation and talk about sequences that would converge if only their limit was in the space we consider Cauchy sequences. It is easy to see that all convergent sequences are Cauchy:
Cauchy sequence
Recall a Cauchy sequence is defined as:
Given a metric space (X,d) and a sequence (x_n)_{n=1}^\infty\subseteq X is said to be a Cauchy sequence[2][3] if:
- \forall\epsilon > 0\exists N\in\mathbb{N}\forall n,m\in\mathbb{N}[n\ge m> N\implies d(x_m,x_n)<\epsilon]
Process
See also
Notes
- <cite_references_link_accessibility_label> ↑ Actually Maurin gives:
- \forall\epsilon>0\exists N\in\mathbb{N}\forall n[n\ge N\implies d(x_n,x)<\epsilon] (the change is the \ge sign between the n and N) but as we shall see this doesn't matter
- <cite_references_link_accessibility_label> ↑ In Krzysztof Maurin's notation this can be written as:
- \bigwedge_{\epsilon>0}\bigvee_{N\in\mathbb{N} }\bigwedge_{n>N}d(x_n,x)<\epsilon
References
- <cite_references_link_accessibility_label> ↑ Krzysztof Maurin - Analysis - Part 1: Elements
- <cite_references_link_accessibility_label> ↑ Functional Analysis - George Bachman and Lawrence Narici
- <cite_references_link_accessibility_label> ↑ Analysis - Part 1: Elements - Krzysztof Maurin