Difference between revisions of "Limit (sequence)"
m (→Process) |
m (→Requiring {{M|x\in X}}) |
||
| Line 51: | Line 51: | ||
==Discussion== | ==Discussion== | ||
===Requiring {{M|x\in X}}=== | ===Requiring {{M|x\in X}}=== | ||
| − | If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}} | + | If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}}. |
| + | |||
| + | To sidestep this limitation and talk about sequences that would converge if only their limit was in the space we consider [[Cauchy sequence|Cauchy sequences]]. It is easy to see that all convergent sequences are Cauchy: | ||
| + | ====[[Cauchy sequence]]==== | ||
| + | Recall a [[Cauchy sequence]] is defined as:<br/> | ||
| + | {{:Cauchy Sequence/Definition}} | ||
| + | {{Begin Theorem}} | ||
| + | [[Every convergent sequence is Cauchy]] | ||
| + | {{Begin Proof}} | ||
| + | {{:Every convergent sequence is Cauchy/Proof}} | ||
| + | {{End Proof}}{{End Theorem}} | ||
| + | |||
===Process=== | ===Process=== | ||
{{Begin Theorem}} | {{Begin Theorem}} | ||
Revision as of 13:46, 5 December 2015
- Note: see Limit page for other kinds of limits
Contents
Definition
Given a sequence [ilmath](x_n)_{n=1}^\infty\subseteq X[/ilmath], a metric space [ilmath](X,d)[/ilmath] (that is complete) and a point [ilmath]x\in X[/ilmath], the sequence [ilmath](x_n)[/ilmath] is said to[1][Note 1]:
- have limit [ilmath]x[/ilmath] or converge to [ilmath]x[/ilmath]
When:
- [math]\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}[n>N\implies d(x,x_n)<\epsilon][/math][Note 2]
- (note that [ilmath]\epsilon\in\mathbb{R} [/ilmath], obviously - as the co-domain of [ilmath]d[/ilmath] is [ilmath]\mathbb{R} [/ilmath])
- Read this as:
- for all [ilmath]\epsilon[/ilmath] greater than zero, there exists an [ilmath]N[/ilmath] in the natural numbers such that for all [ilmath]n[/ilmath] that are also natural we have that:
- whenever [ilmath]n[/ilmath] is beyond [ilmath]N[/ilmath] that [ilmath]x_n[/ilmath] is within [ilmath]\epsilon[/ilmath] of [ilmath]x[/ilmath]
- for all [ilmath]\epsilon[/ilmath] greater than zero, there exists an [ilmath]N[/ilmath] in the natural numbers such that for all [ilmath]n[/ilmath] that are also natural we have that:
Equivalent definitions
- Note: where it is not obvious changes have a [ilmath]\{ [/ilmath] underneath them
[math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[\underbrace{n\ge N}\implies d(x_n,x)<\epsilon\right][/math]
Here we have two definitions
- [math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[n> N\implies d(x_n,x)<\epsilon\right][/math] (given at the top of the page)
- [math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[n\ge N\implies d(x_n,x)<\epsilon\right][/math]
Proof: [ilmath]1\implies 2[/ilmath]
- Let [ilmath]\epsilon >0[/ilmath] be given.
- We know [ilmath]\exists N'\in\mathbb{N} [/ilmath] such that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath] by assuming [ilmath]1[/ilmath] is true
- Choose [ilmath]N=N'+1[/ilmath]
- Now [ilmath]n\ge N\implies[n>N\vee n=N][/ilmath] by definition of [ilmath]\ge[/ilmath], substituting [ilmath]N=N'+1[/ilmath] we get [ilmath]n\ge N'+1\implies[n>N'+1\vee n=N'+1][/ilmath]
- (Case: [ilmath]n>N'+1[/ilmath]) Note that [ilmath]n>N'+1>N'[/ilmath] so by transitivity of [ilmath]>[/ilmath] we see [ilmath]n>N'[/ilmath]
- We know from [ilmath]1[/ilmath] that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath]
- (Case: [ilmath]n=N'+1[/ilmath]), trivially [ilmath]N'+1>N'[/ilmath] so we have so [ilmath]n>N'[/ilmath]
- We know from [ilmath]1[/ilmath] that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath]
- (Case: [ilmath]n>N'+1[/ilmath]) Note that [ilmath]n>N'+1>N'[/ilmath] so by transitivity of [ilmath]>[/ilmath] we see [ilmath]n>N'[/ilmath]
- So in either case we have [ilmath]d(x_n,x)<\epsilon[/ilmath]
- We have shown that if [ilmath]n\ge N[/ilmath] we have [ilmath]d(x_n,x)\epsilon[/ilmath]
- Now [ilmath]n\ge N\implies[n>N\vee n=N][/ilmath] by definition of [ilmath]\ge[/ilmath], substituting [ilmath]N=N'+1[/ilmath] we get [ilmath]n\ge N'+1\implies[n>N'+1\vee n=N'+1][/ilmath]
- Thus choosing [ilmath]N=N'+1[/ilmath] is "an [ilmath]N[/ilmath] that exists" for the given [ilmath]\epsilon[/ilmath]
- This completes the first part of the proof
Proof: [ilmath]2\implies 1[/ilmath]
- Let [ilmath]\epsilon>0[/ilmath] be given.
- We know [ilmath]\exists N'\in\mathbb{N} [/ilmath] such that [ilmath]n\ge N'\implies d(x_n,x)<\epsilon[/ilmath] by assuming [ilmath]2[/ilmath] is true
- Choose [ilmath]N=N'-1[/ilmath]
- Now [ilmath]n> N\implies n>N'-1[/ilmath]
- (Case: [ilmath]n=N'[/ilmath]) if this is the case we know that [ilmath]N'>N'-1[/ilmath] so [ilmath]n>N[/ilmath] is satisfied, but also so is [ilmath]n\ge N'[/ilmath] (we have equality)
- We know from [ilmath]2[/ilmath] that this [ilmath]\implies d(x_n,x)<\epsilon[/ilmath]
- (Case: [ilmath]n>N'[/ilmath]) well [ilmath]n\ge N'[/ilmath] means "if [ilmath]n>N'[/ilmath] or [ilmath]n=N'[/ilmath]" so [ilmath]n>N'\implies n\ge N'[/ilmath], thus [ilmath]n\ge N'[/ilmath]
- We know from [ilmath]2[/ilmath] that this [ilmath]\implies d(x_n,x)<\epsilon[/ilmath]
- (Case: [ilmath]n=N'[/ilmath]) if this is the case we know that [ilmath]N'>N'-1[/ilmath] so [ilmath]n>N[/ilmath] is satisfied, but also so is [ilmath]n\ge N'[/ilmath] (we have equality)
- Now [ilmath]n> N\implies n>N'-1[/ilmath]
- Thus for [ilmath]n>N[/ilmath] we see that [ilmath]d(x_n,x)<\epsilon[/ilmath]
- This completes the proof
(End of proof)
Discussion
Requiring [ilmath]x\in X[/ilmath]
If [ilmath]x\notin X[/ilmath] then [ilmath]d(x_n,x)[/ilmath] is undefined, as [ilmath]d:X\times X\rightarrow\mathbb{R}_{\ge_0} [/ilmath], that is the distance metric is only defined for things in [ilmath]X[/ilmath].
To sidestep this limitation and talk about sequences that would converge if only their limit was in the space we consider Cauchy sequences. It is easy to see that all convergent sequences are Cauchy:
Cauchy sequence
Recall a Cauchy sequence is defined as:
Cauchy Sequence/Definition
Process
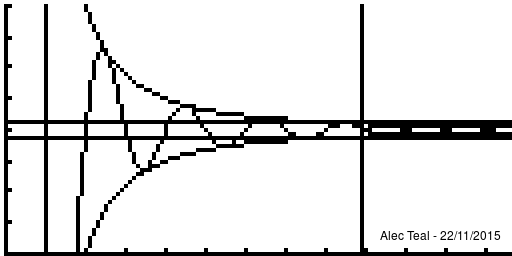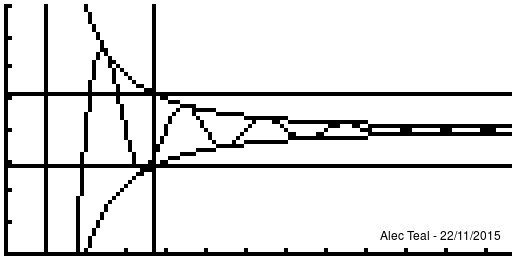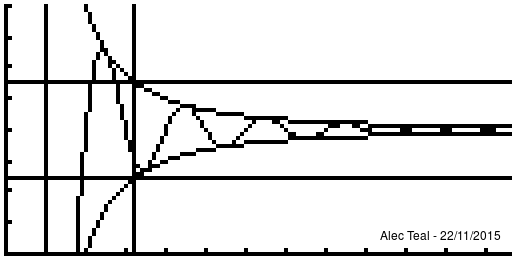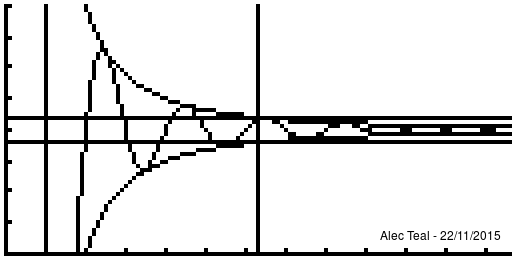
Discussion of why the definition is what it is.
The idea is that defining "tends towards [ilmath]x[/ilmath]" is rather difficult, to sidestep this we just say "we can get as close as we like to" instead. This is the purpose of [ilmath]\epsilon[/ilmath].
We say that "if you give me an [ilmath]\epsilon>0[/ilmath] - as small as you like - I can find you a point of the sequence ([ilmath]N[/ilmath]) where all points after are within [ilmath]\epsilon[/ilmath] of [ilmath]x[/ilmath] (where [ilmath]d(\cdot,\cdot)[/ilmath] is our notion of distance)
- That is after [ilmath]N[/ilmath] in the sequence, so that's [ilmath]x_{n+1},x_{n+1},\ldots[/ilmath] the distance between [ilmath]x_{N+i} [/ilmath] and [ilmath]x[/ilmath] is [ilmath]<\epsilon[/ilmath]
- This is exactly what [ilmath]n>N\implies d(x_n,x)<\epsilon[/ilmath] says, it says that:
- whenever [ilmath]n>N[/ilmath] we must have [ilmath]d(x_n,x)<\epsilon[/ilmath]
- This is exactly what [ilmath]n>N\implies d(x_n,x)<\epsilon[/ilmath] says, it says that:
As per the nature of implies we may have [ilmath]d(x_n,x)<\epsilon[/ilmath] without [ilmath]n>N[/ilmath], it is only important that WHENEVER we are beyond [ilmath]N[/ilmath] in the sequence that [ilmath]d(x_n,x)<\epsilon[/ilmath]
Notice that at [ilmath]x=1[/ilmath] that , in fact the curve is within [ilmath]\pm\epsilon[/ilmath] several times before we reach the vertical line, this is the significance of the implies sign, when we write [ilmath]A\implies B[/ilmath] we require that whenever [ilmath]A[/ilmath] is true, [ilmath]B[/ilmath] must be true, but [ilmath]B[/ilmath] may be true regardless of what [ilmath]A[/ilmath] is.
Note that after the vertical line the function is always within the bounds.
Because of this any [ilmath]N'>N[/ilmath] may be used too, as if [ilmath]n>N'[/ilmath] and [ilmath]N'>N[/ilmath] then [ilmath]n>N'>N[/ilmath] so [ilmath]n>N[/ilmath] - this proves that if [ilmath]N[/ilmath] works then any larger [ilmath]N'[/ilmath] will too. There is no requirement to find the smallest [ilmath]N[/ilmath] that'll work, just an [ilmath]N[/ilmath] such that [ilmath]n>N\implies d(x_n,x)<\epsilon[/ilmath]
See also
Notes
- ↑ Actually Maurin gives:
- [math]\forall\epsilon>0\exists N\in\mathbb{N}\forall n[n\ge N\implies d(x_n,x)<\epsilon][/math] (the change is the [ilmath]\ge[/ilmath] sign between the [ilmath]n[/ilmath] and [ilmath]N[/ilmath]) but as we shall see this doesn't matter
- ↑ In Krzysztof Maurin's notation this can be written as:
- [math]\bigwedge_{\epsilon>0}\bigvee_{N\in\mathbb{N} }\bigwedge_{n>N}d(x_n,x)<\epsilon[/math]
References
- ↑ Krzysztof Maurin - Analysis - Part 1: Elements